おとといのジョーの部屋
　

ようこそ！　おとといのジョーの部屋へ，フラクタル絵画をどうぞ

Welcome to the world of mathematical pictures

Vienvenidos al mundo de pinturas matemáticas

　　　　　 　　　　　　　　　　　　　　１．複素関数の数列が描く絵画を紹介！(目次へ)
　　　　　　　　　　絵の作り方：　・複素関数　f(z)， z:complex　　による反復。
　　　　　　　　　　　　　　　　　・ f(z) は 多項式，有理関数，超越整関数など（パラメーターを含む）。
　　　　　　　　　　　　　　　　　・ 数列　z n=f n(z0),  z0 ; given, n=1,2, … 　がどのような 振る舞い
　　　　　　　　　　　　　　　　　　をするかによって初期値 z0 に色をつける（Julia集合，Fatou集合）。
　　　　　　　　　　　　　　　　　・パラメーターに依存して決まる 臨界点や特異値を初期値にした数列が，無限遠点に
　　　　　　　　　　　　　　　　　　発散しないようなパラメーターの領域を黒色で表示（Mandelbrot集合）。
　　　　　　　　　　　　　　　　　・ 計算プログラムは 十進BASIC を用いる。
　　　　　　　　　　Key words: Complex Dynamics, Julia Set, Fatou Set, Mandelbrot Set, Entire Functions.

　　　　　　　　　　　　　　　　　　　２．中・高生のための数学勉強部屋（ファイルをダウンロードして使ってね）
　　　　　　　　　　　　・令和2年 神奈川県公立高校入試問題（数学）の略解と解説　……　おとといのジョーの独断と偏見
　　　　　　　　　　　　・令和3年 神奈川県公立高校入試問題（数学）の略解と解説　……　ことしの試験の難易度は？
　　　　　　　　　　　　・テキスト１；絵とともに学ぶ中学数学「数・式の計算・関数・方程式」　
　　　　　　　　　　　　・テキスト２；絵とともに学ぶ中学数学「平面図形とその応用」　
　　　　　　　　　　　　・テキスト３；絵とともに学ぶ中学数学「空間図形，確率・統計」　

　　　　　　　　　　　　・令和4年 神奈川県公立高校入試問題（数学）の略解と解説　……　コロナ禍の中，勉強の成果は？
　　　　　　　　　　　　・令和4年 東京都公立高校入試問題（数学）の略解と解説　……　東京都の問題は初解説，難易度は？

　　　　　　　　　　　　・令和5年 神奈川県公立高校入試問題（数学）の略解と解説　　……　問題は去年より難しかったね。
　　　　　　　　　　　　・令和5年 東京都立高校入試問題（数学）の略解と解説　　……　超・難問がきついね。他はやさしい。

　　　　　　　　　　　　・中・高生のための数学読本:数とはなんぞや --数は誰が作ったの,どこにあるの--　……　テキストだよ　
　　　　　　　　　　　　・中・高・大学生のための　パイソンでグラフを描こう　……　プログラミングのお手伝い！　

　　　　　　　　　　　　・令和2年 大学入試センター試験（数学U・数学B）の略解と解説　……　歯にころもきせぬ解説
　　　　　　　　　　　　・令和3年　大学入試共通テスト （数学U・数学B）の略解と解説　……　共通テスト元年，難易度は？
　　　　　　　　　　　　・「漸化式を含む差分方程式の解について」（高校生のための参考資料）
　　　　　　　　　　　　・令和4年 大学入試共通テスト（数学T・数学A）の略解と解説　……　過去最低の平均点？難しかったかな
　　　　　　　　　　　　・令和4年 大学入試共通テスト（数学U・数学B）の略解と解説　……　平均点低かったね？2年目の問題はいかに

　　　　　　　　　　　　・令和5年 大学入試共通テスト（数学U・数学B）の略解と解説　……　問題は比較的やさしかったね。
　　　　　　　　　　　　・令和5年 大学入試共通テスト（数学I・数学A）の略解と解説　……　不定方程式は2年連続でたね。

　　　　　　　　　New ・令和6年 大学入試共通テスト（数学I・数学A）の略解と解説　……　難しくはなかったけど，慣れない問題がでたね。
　　　　　　　　　New ・令和6年 大学入試共通テスト（数学U・数学B）の略解と解説　……　例年よりやさしかったけど，できたかな。

　　　　　　　　　　　　・「令和3年　開成中学校入試問題（算数）」考　― 略解と解説をふまえて―　……　中学入試に物申す

　　　　　　　　　　　　　　　　　　　３．おとといのジョーの独り言（社会にモノ申す！）
　　　　　　　　　　　　・日本のプロ野球をもっと面白くして　．．．　クライマックスシリーズは即中止，東アジアリーグの提言
　　　　　　　　　　　　・原発はやめようよ　　　　　　　　 ．．．　原子力は，人が制御できない代物と思うべし
　 　　　　　　　　　　　・日本が世界をリードしようよ　　　．．．　アメリカから独立し，永世中立国をめざせ
　　　　　　　　　　　　・横浜市のIRカジノ構想に反対　　　．．．　横浜市長は市民を馬鹿にしていませんか
　　　　　　　　　　　　・プーチンさん戦争はやめましょう！．．．　史上最悪の侵略戦争。Stop War immediately!

　　　　　　　　　　　　・我が家の愛犬　チコちゃん　　　．．．　写真をどうぞ!!
　　　　　　　　　　　 　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　by

　　　　　　　　　　　　　　　　　　　　　　　一昨日　冗　（ ototoi no joe ; pen name ）
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 作成日； 6月23日, 2019
　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　 　 33回目のアップデート；3月16日，2024
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 34回目のアップデート; 4月5日, 2024

　　　第1ルーム　フラクタル絵画(Fractal Pictures)
　　　　　　P-I.　多項式(Polynomials)　．．．Julia Set, Fatou Set の一般的性質
　　　　　　P-2. 2次関数(Quadratic Polynomial)　．．．元祖 Mandelbrot集合などは，皆さんご存じと信じ，詳細は略
　　　　　　P-4. 4次関数(Quartic Polynomial) 　．．． Mandelbrot集合の定義から説明，かなり詳しい内容になってるよ
　　　　　　E-I. 超越整関数(Entire Functions)　．．．Mandelbrot集合の定義や一般的性質
　　　　　　　　　　E-1. 指数関数(Exponential function)　．．．カントールの花束きれいだね
　　　　　　　　　　E-2. 三角関数ともう1つの指数関数(Trigonometric function)　．．．Fatou Sets の形トゲだらけだね
　　　　　　E-S. すてきな絵(Nice pictures)　．．．私の持っている素敵な絵をのせます
　　　　　　R-ex. ある有理関数(A Rational function)　．．．1つの有理関数の詳細を解析
　　　　　　F-o. 公開ファイル(Open program files)　．．．BASICプログラム；使ってくれると嬉しいね

　　　第2ルーム　中・高生のための数学勉強部屋(Mathematical study room for students)
　　　第3ルーム　おとといのジョーの独り言（社会にモノ申す！）(My opinions)

P-I. 多項式

　　　　f(z) が多項式のとき，無限遠点∞ は超吸引的固定点。f '(c)=0 を満たすc は臨界点（critical point），f(c) は臨界値（critical value）
　　である。吸引的固定点 p に収束する初期値の集合　　Ws(p)={ z |　f n(z) → p　(n → ∞ ) }　　は p の吸引的鉢 （attractive basin or
　　stable set）と呼ばれ，この集合に属すp を含む成分を p の直接鉢（immediate stable set）といい A(p) とかく。多項式の場合
　　A(∞)=Ws(∞)　である。以下の定理は絵を理解する上で重要：
　　定理１． 直接鉢 A(p) は少なくとも１つの臨界値を含む。
　　定理２． ∞ を除く全ての臨界点が A(∞) に含まれるならば， ジュリア集合 J は完全不連結（totally disconnected）であり，カントール
　　　　　　集合と位相同型である。
　　定理３． f(z) は次数d の多項式とする。有限な非反撥的周期軌道の数は，高々 d-1 である。
　　　　　数列が無限遠点∞ に発散しない初期値の集合　　K(f)={ z |  f n(z) —⁄→ ∞  (n → ∞ ) }　　を充填ジュリア集合という。また，
　　関数 f(z) のファトゥ集合は F で表す。尚，複素力学系（complex dynamics ）で現われる種々の専門用語の定義や，結果としての定理
　　などは次の文献を参照せよ：

　　　　　　　 [1] 上田 哲生，谷口 雅彦，諸澤 俊介；　複素力学系序説，培風館(1995)
　　　　　　　 [2]　P.Blanchard; Complex Analytic Dynamics on the Riemann Sphere, Bull.of AMS. 11-1(1984) pp.85-141
　　　　　　　 [3] 一昨日 冗；　十進BASICで方程式を遊ぶ，東京図書出版(2014)

P-2. 2次関数

　　　　一般の2次関数　az2+bz+c　は　f(z)=z2+α　と解析的共役（analytically conjugate）なので，この f(z) で話を進める；
　　　　 　　　　　　　　　　f(z)=z2+α, 　　　(α はアルファ，フォントよくないね)．　　　　　　　　　　　　　　　　　　　　　　(p.1)
　　f(z) のマンデルブロー集合は　　M={ α | 0 ∈ K(f) }　　と定義される。この集合はパラメーターα の 空間である。 M の全体図や性質など
　　は文献 [3] pp.151-155 を参照せよ。K(f) が連結であることと　α ∈ M　と は同値である。ここで， M のある微小部分と，そこに含まれる
　　１つの α に対する f(z) のジュリア集合およびファトゥ集合の図を見てみよう。

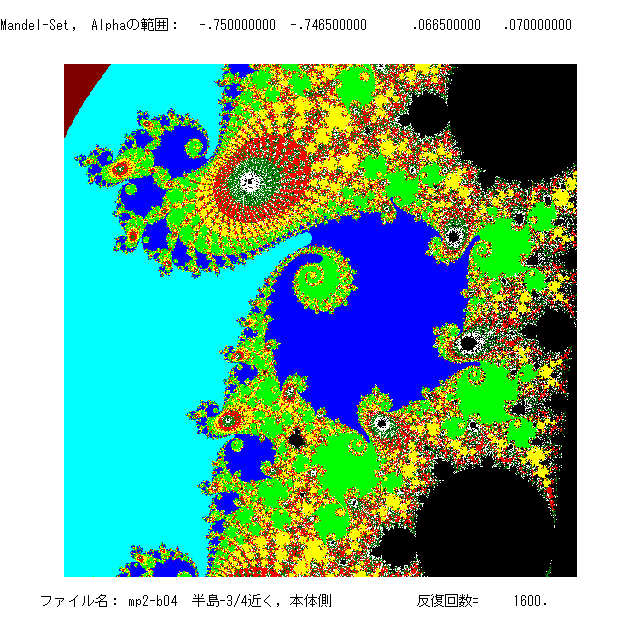
　　　　　　＜図の説明＞
　　 mp2-b04: 　マンデルブロー集合 M の微小部分（α=-3/4 の右上
あたり）で，領域は [-.75, -.7465]×[.0665, .07] である。黒の領域
がマンデルブロー集合。飛び地のように黒の領域があるがすべてつな
がっている。即ちマンデルブロー集合は連結。黒以外の色が付いている
部分は {f n(0)} が無限大に発散する α の領域。反復回数とは，その
回数までの反復で発散しない数列は α ∈ M とみなすという意味である
（理論とのずれが生じている）。色は，初めて |f N(0)|>2 となったNが
　　　　　　bi≤ N < bi+1 　　　 (i=1,2,… ,7)
のとき，α に同じ色をつける。b8 は反復回数で
　　　　　　bi=int( bi+1/1.66+.5 ) 　　　 (i=7,6,… ,1)
を満たす。この図の右上の黒い部分（雪だるまの胴体）にあるパラメー
ターα は周期45の吸引的周期点をもつパラメーターである。同様に右下
の雪だるまの胴体部分は周期47の吸引的周期点をもつ領域である。

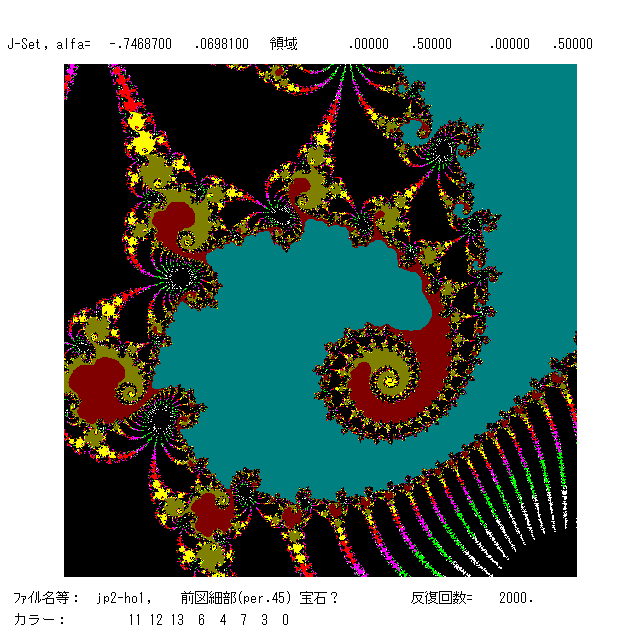
　　 jp2-h0: α=-.74687+.06981i のときの z平面上の図で，周期45
の吸引的周期点をもつケースである。図の領域は四角形 [-1.4, 1.4]×
[-1.4, 1.4] 。黒の領域の境界がジュリア集合 J，ジュリア集合で囲ま
れた無数の領域（黒の部分）はファトゥ集合 F。ファトゥ集合は無限個
の連結成分よりなる。黒以外の色の付いている領域は ∞ に発散する領
域，即ちファトゥ成分 A(∞) である。このA(∞) は1つの単連結領域で
ある。色の付け方はマンデルブロー集合の場合と同じである。
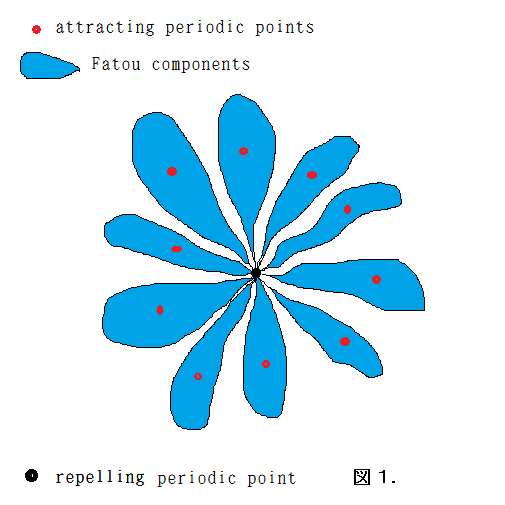
　　黒の楕円形のような領域に，櫛の歯のような枝がぐるーっと連なっ
ているいる模様が見えるが，これらの枝は楕円の中央までずーっと伸び
て1点（反撥的周期点）で繋がるのである。図１（これは周期10 の場合）
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　を参照せよ。この絵のように，1点を中心に45枚の（ファトゥ成分の）
　　葉が並んでいなければならないのである。理論と現実の計算のギャップがこういう所に現れている。全平面 C は A(∞) と J と黒のファトゥ成分から
　　成る。周期45の吸引的周期点は，図の左側（ Re(z)<0 の方）の一番大きな45枚のファトゥ成分の中に入っている。

　　 　 jp2-ho1: 前図の細部で領域は [0, .5]×[0, .5] である。櫛の歯の形が良く見え，螺旋形の
奥深くまで仏舎利塔のような構造物が無限に連なっている美しい絵である。いわゆるフラクタル図
形のあでやかさをとくとご覧あれ。
　　　　　　　　　　　　　　＜図説明エンド＞




　さて，次にジュリア集合 J がカントール集合のときの絵をのせよう。このケースは C=J ∪A(∞)
であり，A(∞) は無限連結である。カントール集合は点の集合なので，正確な図を作るのは困難で
ある。なぜなら，点は面積ゼロだからである。近似の図で比較的見ばえのするものは文献 [3] の
p.146 に２つあるので参考にして欲しい。A(∞) に色付けした絵では，カントール集合がどこにあ
るかはほとんど分らない。しかしながら，A(∞) の紋様を楽しむことができる。


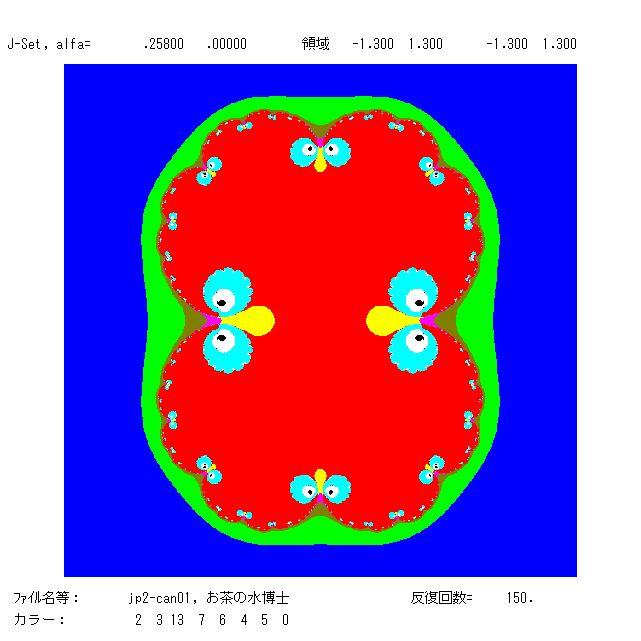
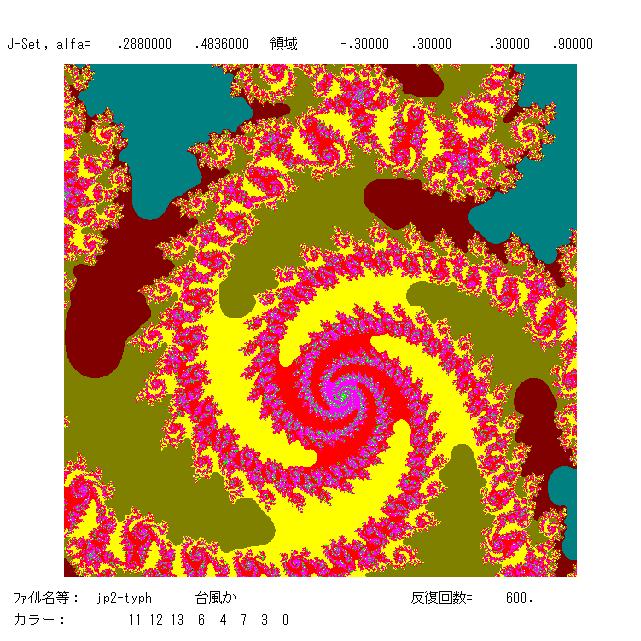
　　左の絵と真ん中の絵は同じパラメーター α=.258 のもの。鉄腕アトムのお茶の水博士を連想しますが，いかが。カントール集合は白の領域
　　内にあるが，想像できますか。右の絵は α=.288+.4836i のもので，北半球の台風のようです。自己相似なフラクタル図形がみごとです。

このページのトップに戻る 　第1ルームの目次に戻る

P-4. 4次関数

　　　　方程式は
　　　　　　　　 　　　　　　　f(z)=z4 - 2pz2 + 4qz + b, 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(p.2)
　　ここに， p=(a1+a2)2 - a1a2,　 q=a1a2(a1+a2). そして　a3= - (a1+a2)　 とおけば，f(z) の 臨界点は a1, a2, a3 である。この方程式の
　　パラメーター空間は　H={ (a1, a2, a3) | a1+ a2+ a3=0 } 　とおけば， H×C である。2次関数のマンデルブロー集合のような集合は，
　　臨界点の軌道 O+(a i)　( i=1, 2, 3 )　が発散するかしないかで類別できる。発散を1，発散しない（収束を含む）を 0 とおけば，
　　(O+(a1), O+(a2), O+(a3) ) の最終状態として次の８つのケースがあり，それぞれ の場合に対応してパラメーター空間に異なる色をつける；
　　　(0,0,0)　黒，　(1,0,0)　白，　(0,1,0)　水色，　(0,0,1)　紫，　(1,1,0)　赤，　(1,0,1)　緑，　(0,1,1)　黄色，　(1,1,1)　青．
　　　
　　　　実際には，パラメーター空間 H×C に直接色をつけることは不可能なので，例えば a1, a2 を固定して b 平面に絵を描くか，a1, b を固
　　定して a2 平面に絵を描くかすればよい。これら２つの図を，ここでは 4次マンデルブロー集合とよぶ。z 平面上のファトゥ集合（ジュリア
　　集合）を描く場合は，すべての初期値z0 に対して，その軌道が発散するときに色をつけ，発散しないとき黒とする。
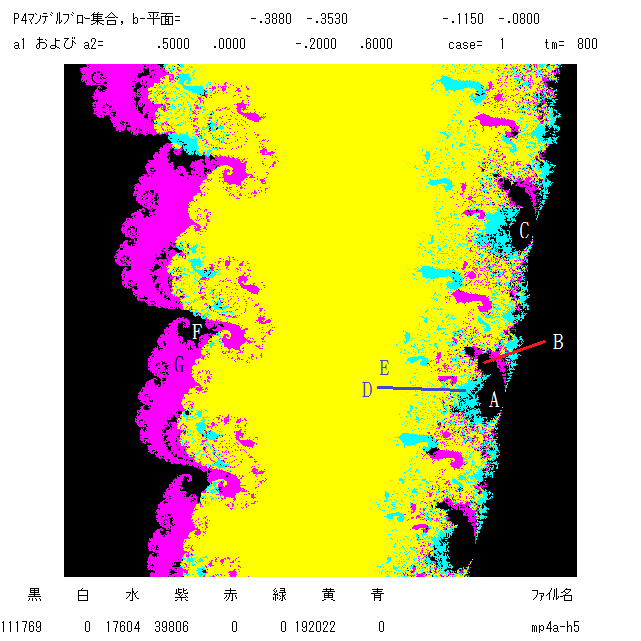
　　　　次の2つの図は，a1= .5, a2= -.2 + .6 i のときのマンデルブロー集合である（b平面上の図）。 左の全体図の一部分が右の図である。



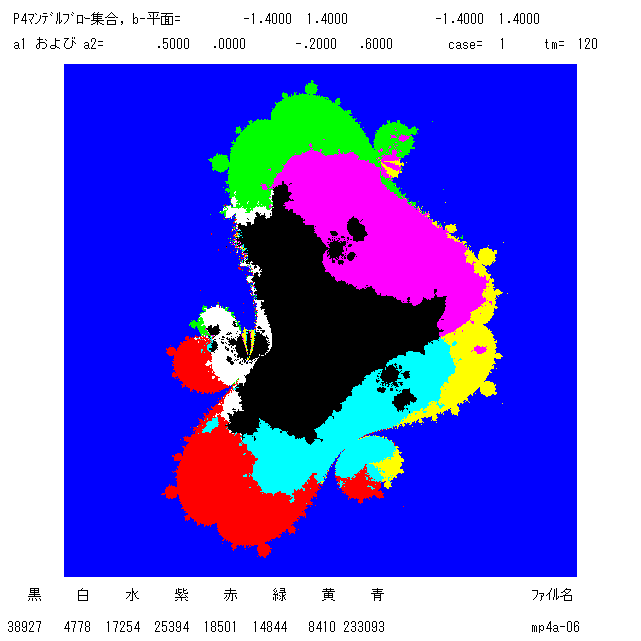
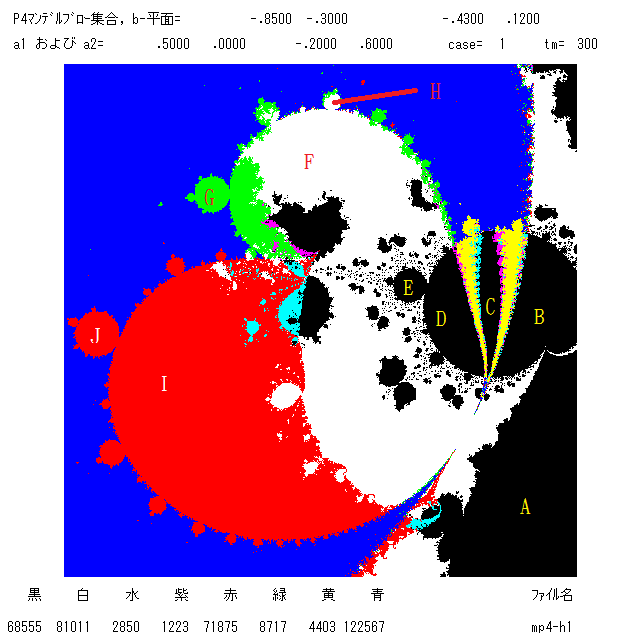
　　右図の中の2本の牙（セイウチの牙？）は場違いの所に出ているように見え，不思議な形です。このあたりで何が起こって いるか見てみよう。
　　３つの臨界点の軌道　O+(a i)　( i=1, 2, 3)　の行き着く先がどこかを表で示す。右図の中に書き込まれた点 A から点 J が示す b の値に対す
　　るものである。
　 　　
表１
　軌道⇓ 点⇒　 A B C D E F G H I J
　O+(a1) 固 周2 周2 周2 周4 ∞ ∞ ∞ ∞ ∞
　O+(a2) 固 固 周2 周2 周2 周2 周4 周8 ∞ ∞
　O+(a3) 固 固 周2 周2 周2 周2 ∞ 周8 周2 周4

　　　　表の中の，“固”は吸引的固定点，“周ｋ”は周期ｋの吸引的周期軌道を表し，“∞”は無限遠点への発散を意味する。また，同じ周期で同色の
　　活字は同じ軌道を表し，異なる色の活字は異なる軌道を表す。例えば，点Aでは３つの軌道が1つの固定点に収束する。点Dでは周期2の軌道が
　　２つあって，O+(a2) と O+(a3) が同じ軌道に収束するということを示している。２本の牙の周りでは力学系が少しずつ違っているのに気付き
　　ましたか。さて，２本の牙のごく近くを見てみよう。牙の根もと付近を拡大しました：



　　　　牙の周りの紋様は，南国の島の周りのサンゴ礁のようなきれいな形を見せてくれています。このあたりで何が起こっているか，再び臨
　　界点の軌道を追っかけよう。
　 　　
表２
　軌道⇓ 点⇒　 A, B C D E F G H I J KL
　O+(a1) 周2 周2 周2 周2 周2 周2 周2周2周2周2周2
　O+(a2) 周33 周31 ∞ ∞ 周2 周2 周2 ∞ ∞ 周26 周2
　O+(a3) 周33 周31 周33 ∞ 周2 ∞ 周2 周2 ∞ ∞ ∞

　　　　牙の内側の水色と紫色の部分は共に周期2で大きな周期は持たないこと，そして牙の外側の部分には周期の大きな吸引的周期点をもつ
　　領域があることが分る。例えば，点A,B では周期33，点C では周期31，点K では周期26をもつ。どうしてこのような構造になっているの
　　かは説明できないね。さて，Z平面上のジュリア集合，ファトゥ集合の絵を２つのせる：



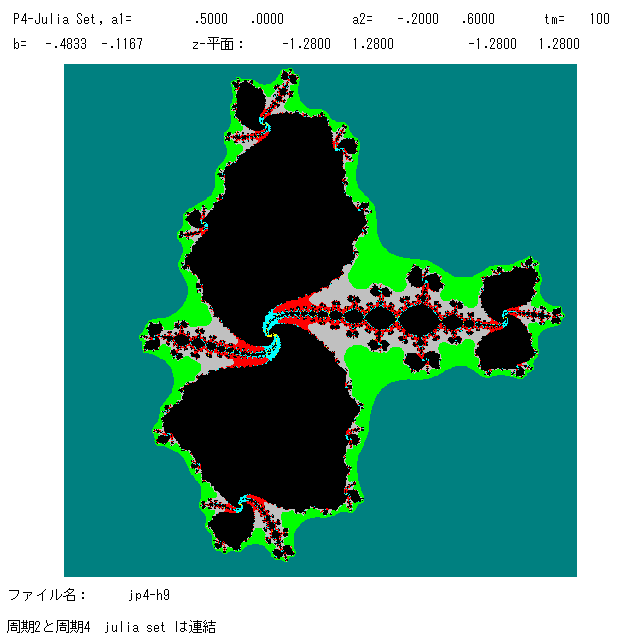
　　　　左の図は，表1の点E の位置の b を用いたときのジュリア集合，ファトゥ集合の絵である。吸引的な周期2と周期4の軌道が共存してい
　　るケース；O+(a1) は周期4に収束し，O+(a2) と O+(a3) は １つの周期2の軌道に収束する。従って，ファトゥ成分は2種類存在する。蝶の
　　羽のような2枚の羽から成っている成分が周期2のもので，玉がつらなっているような成分は周期4のものである。同じ黒の成分でもその形
　　から容易に類別できる。ジュリア集合は連結なので，A(∞) は単連結である。
　　　　右の図は，表2の点D の位置の b を用いたときのもの。 O+(a2) は発散するので， A(∞) は無限連結，無限連結の穴となっているのが
　　周期2のファトゥ成分と周期33のファトゥ成分である（この緑の部分は私の予測であって証明されていない事柄かもしれない）。周期2の
　　周期点は左右のやや大きな黒の成分（マンタ or 鯨のような形）の中にある。周期33のファトゥ成分は，反撥的周期点を中心にした33枚の
　　花びらからできているのであるが，正確には描ききれない。櫛の歯のような形がどうしても残ってしまう。2種類のファトゥ成分はもちろ
　　ん連結していない。
　　　　ここでは，カラーは黒以外6色しか使っていない。反復回数 tm を b7，　bi=int ( 0.52× bi+1+.5 ) 　 ( i=6, 5,… , 1)　とおき，
　　初めて　|f N(z0)|>2　 となった N が　bi≤ N < bi+1 　( i=1, 2,… , 6)　にあるとき， 初期値 z0 に同じ色をつける。2次多項式の場合と
　　は少し違う。

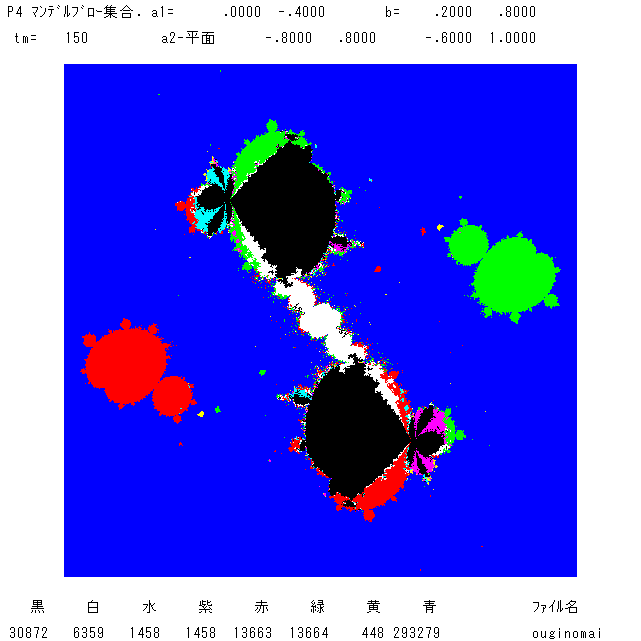
　　　　（追記　7.1 '20）ここで，a1とbを固定した，マンデルブロー集合を２つ持ち出そう。a2平面での絵である。 左図は，私が「扇の舞」と
　　呼んでいるもので，那須の与一に射られた平家方の扇の海に落ちるところが連想されます。まあ，面白い形です。右の図は 「毒蛾」（どくが）
　　と呼んでいます。絵は点対象ですが，蝶に見えないことはない。



　　　　下の2枚の絵は，上の2枚の絵からパラメーターを選んだときの，ジュリア集合（黒と色のついている領域の境界）の絵である。共にパラメーター
　　は白の領域から選んでいる。O+(a1) → ∞ , O+(a2) と O+(a3) は １つの吸引的周期軌道に近づく。A(∞) は，共に無限連結だよ。


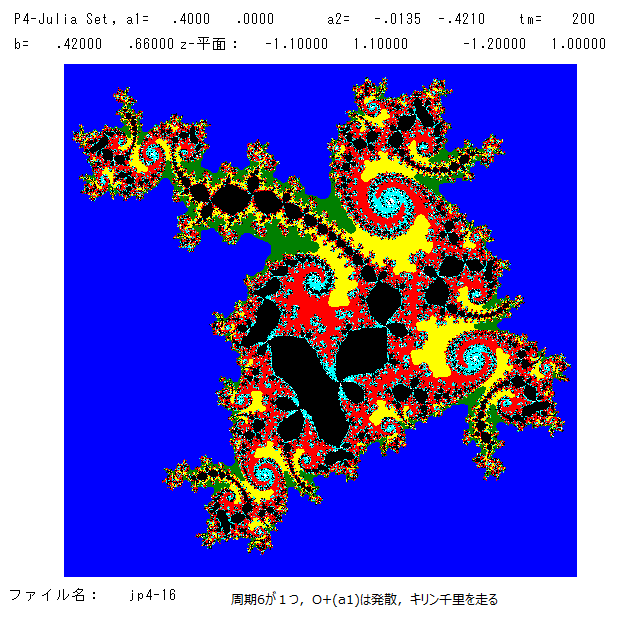
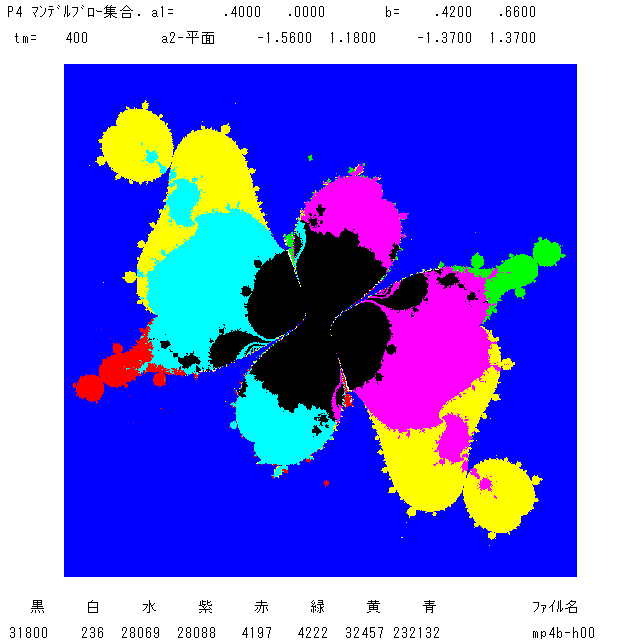
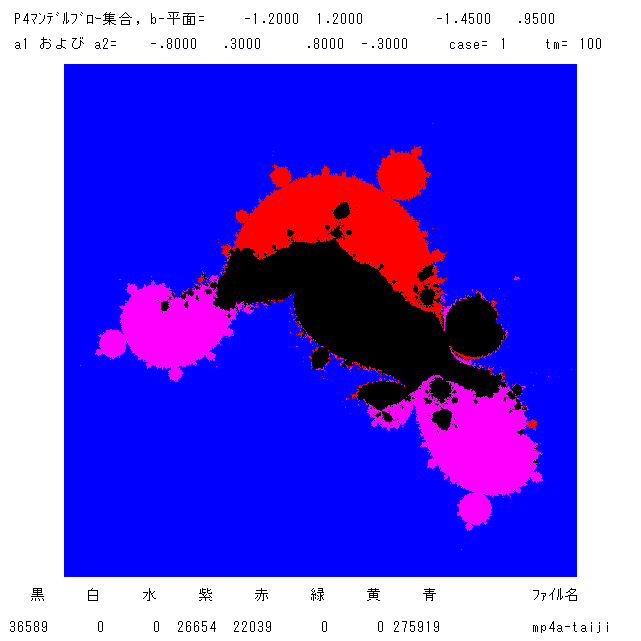
　　　　（追記　1.4 '21) a1とa2を，a1=-0.8+0.3i, a2=0.8-0.3i に固定したマンデルブロー集合 を2枚のっけます。b平面上の絵です。左図は，文献[3]で一度
　見せたものですが素晴らしい絵なのでここで再び取り上げます。私はこれを胎児(unborn baby)と呼んでいます。 完全には成長していない胎児，しかしほぼ人
　であることは明白です。あなたの目にはどう映りますか？　おへそもあるししっぽもついてますね。
　　胴体・右腕・足の黒い部分からパラメーターbを選ぶと，吸引的固定点が１つです。頭は吸引的周期2が1つ，左手(黒いヒレのような部分)は周期3， おへそは
　周期4です。即ちこれら黒の部分からbを選んだとき，O+(ai) (i=1,2,3) はすべて1つの吸引的軌道(固定点を含む)に 収束します。紫の大きい領域は固定点が１つ。
　O+(ai) (i=1,2) が収束，O+(a3) は発散。それにくっついている一番大きい雪だるまの 胴体は周期2だよ。
　　背の上にある赤の大きい領域では O+(a3) が固定点に収束し，O+(ai) (i=1,2) は発散する。これに くっついている一番大きい雪だるまの胴体は周期2の領域。
　右腕の脇の下あたりに小さな黒の心臓形があるが，ここを拡大したのが右図です。心臓形であることは拡大して見て やっと分かるね。このカージオイドは特別
　な場所のようです。1,3 の数字が入っている部分は，O+(ai) (i=1,2) が固定点 に収束し，O+(a3) が周期3の周期軌道に収束することを意味します。1,6 と 1,9
　も同様の状況を示します。単に，1 や 3 が入っている黒の領域は，その周期の吸引的周期軌道が１つあることを示します。



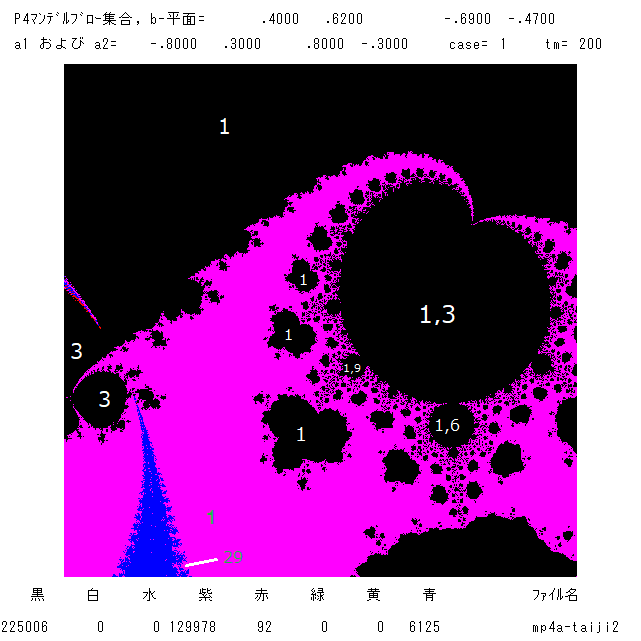
　　上の左図の右やや下に小さな赤の雪だるまが見えると思いますが，これの胴体は周期2の領域です。この雪だるまのすぐ左にある紫の領域(周期７) からbを
　選んだ時のジュリア集合の絵が下図左のものです。ありきたりの絵ですが，連結したファトゥ成分の塊が まあまあきれいです。右図は，上図右の 1,6 の領域
　からbを選んだときのジュリア集合の絵です。周期1と周期6のコラボレーションで，周期1の宇宙（ファトゥ成分）を周期6のファトゥ成分がつないでいます。
　ちょっと面白い構造です。


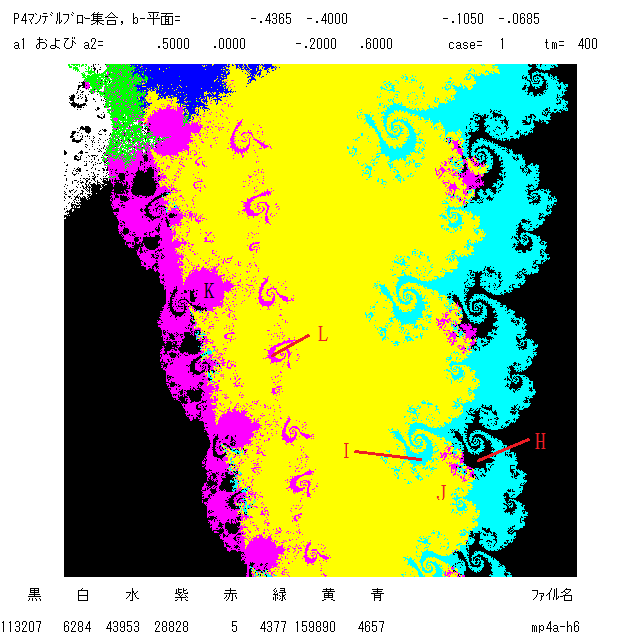
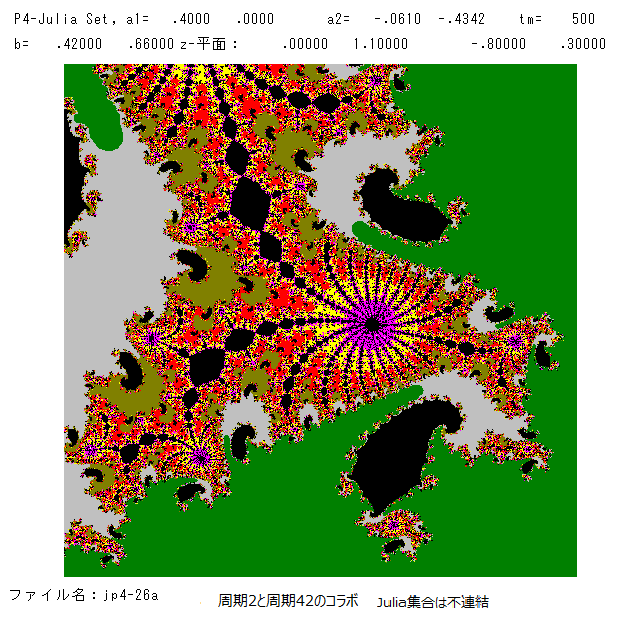
　　　　（7月8日 '21 追記）ジュリア集合の絵を2枚のっけます。下図左は，マンデルブロー集合の青の部分からパラメーターを選んだ。臨界点の軌道は
　　O+(a1)は，周期42の周期点に近づき，O+(a2)は発散，O+(a3)は周期2に 近づく。従って，ジュリア集合は不連結である。
　　　　下図右のものは，上図右の小部分（中央やや左上部分）の絵である。連結したファトゥ成分がまあまあきれいですね。



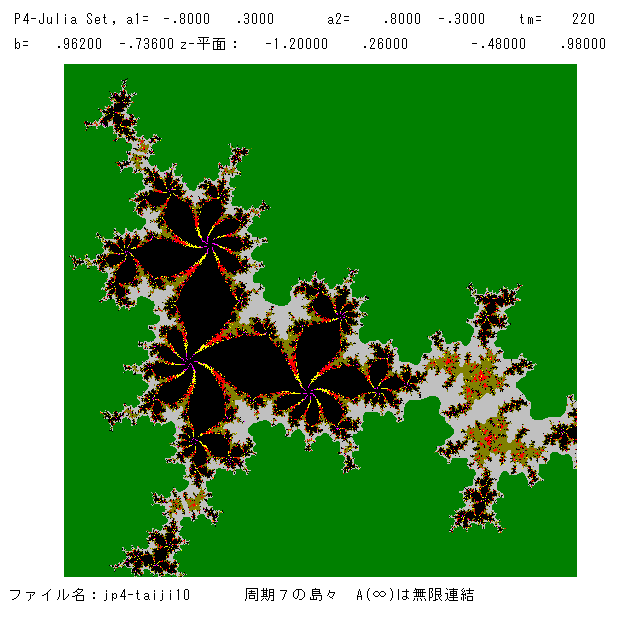
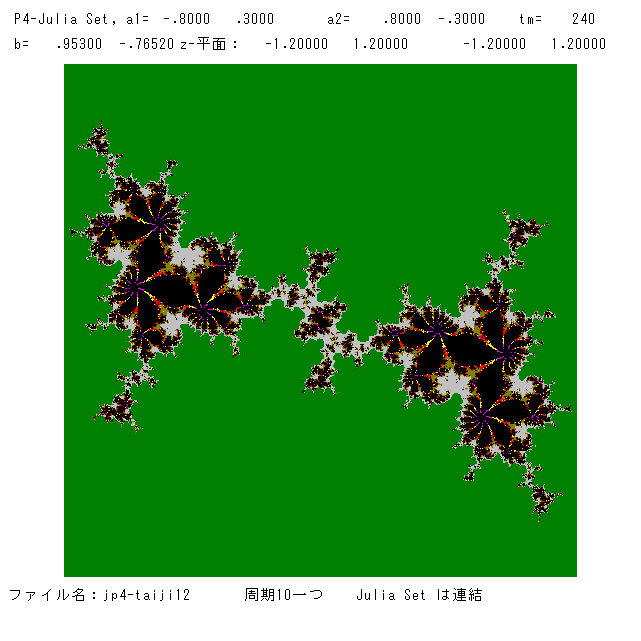
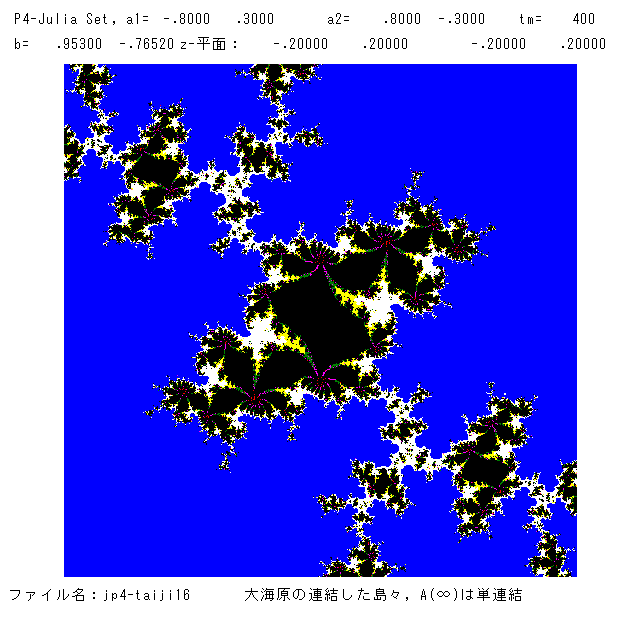
　　　　（11月23日 '21 追記）マンデルブロー集合「胎児」（mp4a-taiji）から1点
　　　　　　　a1=-0.8+0.3i, a2=0.8-0.3i, b=0.953-0.7652i
　　を選び（「胎児」の右下の小さな赤い雪だるまの，やや左下の紫の領域の中の黒い部分の1点）ジュリア集合の絵を描いてみました。安定な周期点は周期10
　　のものが１つで，すべての臨界点の軌道はこれに近づきます。即ち，ジュリア集合は連結で，A(∞)は単連結です。単純な力学系ですが，連結したファトゥ
　　成分がきれいです。左図が全体図で，右図が原点近傍の 小さな領域です（カラーは変えました）。大海原の中の無数の島々を連想させます。1つの絵は，
　　よく観察するときれいな部分が必ずあります。人間と同じですね。どんな人も必ず素敵な良い所をもっています。


このページのトップに戻る 　第1ルームの目次に戻る
　

E-I. 超越整関数

　　　　f(z) が e z, sin z, cos z 等を含む超越整関数（transcendental entire function）のときのジュリア集合・ファトゥ集合 の絵を描こう。
　　超越整関数では，臨界値の軌道と共に特異値（asymptotic value） の軌道の振る舞いが力学系の多くを決定してしまう。拡張された複素数
　　平面 C∪{∞} 上の点 w が f(z) の特異値とは，
　　　　　　　lim t→ ∞ r(t) = ∞ 　をみたす１つの連続曲線 r(t) があって， lim t→ ∞ f(r(t)) =w
　　となるような w である。この特異値については文献 [1] では定義が異なるので注意のこと。Re(z) → - ∞ となるような任意の曲線は上の定
　　義を満たす曲線なので，0 は e z の特異値である。尚，超越整関数に関する多くの結果については，[1] と次の文献を参照されたい：

　　　　　　[4] R.L.Devaney; Complex Dynamics and Entire Functions. Pro. of Symposia in Applied Math. Vol.49:
　　　　　　　　　　　　　　　Complex Dynamical Systems, A.M.S, pp.181-206 (1994)
　　　　　　[5] R.L.Devaney; An Introduction to Chaotic Dynamical Systems. Second Ed. Addison-Wesley, pp.319-328 (1989)

　　さて，　If ={ z∈C　 | 　 lim n→ ∞ f n(z) = ∞　 }　を発散点集合とよぶ。 超越整関数についての以下の定理は絵を理解するのに役立つ。
　　定理４．点 z0 が吸引的周期点またはハイパボリック周期点の1点ならば， 臨界点の軌道または特異値の軌道の少なくとも１つは，z0 の軌道
　　　　　 O+(z0) に近づく。
　　定理５．超越整関数のジュリア集合は C の非有界集合である。
　　定理６． f(z) のジュリア集合を J とすると，J=∂If が成立する。
　　定理７． ∞ に至る曲線 Γ 上で f(z) が有界ならば，ファトゥ集合 F のすべての成分は単連結である。

　　　　超越整関数の安定領域（ファトゥ成分）では，多項式や有理関数では現れなかった遊走領域（wandering domains） とベーカー領域
　　（Baker domains）というものがある。これらは，後ほど絵で説明する。

E-1. 指数関数

　　　　c をパラメーターとした指数関数
　　　　　　　　　　　　f(z) = c ez　　（ c=a+b i ）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(e.1)
　　の力学系を考える。まず最初に，2次関数のときのマンデルブロー集合に相当する分岐図を描こう。指数関数には臨界点はなく，特異値 0 が
　　あるのみなので，c 平面上の集合
　　　　　　　　　　　Me={ c |  f n(0) —⁄→ ∞ (n → ∞ )　 }
　　が2次関数のマンデルブロー集合と同等の図である（我々はこれを指数関数 (e.1) のマンデルブロー集合とよぶ）。以下の絵ではMe は黒で，
　　色の付いている領域は ∞ に収束する領域である。Im(c)>0 の部分にあるマンデルブロー集合の絵を２つ示す：



　　　　左の図の黒の領域の数字n(=1,2, … ,8) は，その領域のパラメーターc を選べば安定な周期nの周期軌道をもつ， と言うことを示して
　　いる。赤の数字は赤線の先の領域がその数の周期軌道をもつということである。黒の領域（例えば 2 と4）は連結しているように見えるが，
　　色の付いているフラクタルな曲線によって分けられている。色の付いている領域は ∞に収束する領域だが，これの判定は実はとても難しい。
　　コンピューターによる計算は有限の世界であり，数学は無限の世界であるからである。だから絵は正しくないのだが，大まかな絵としては
　　これでいいのである。例えば 4 の領域は右の方へ行くと緑の舌のような領域にぶつかってしまうが，実は緑の舌にはぶつからずに黒い領域
　　が帯または糸のような形になり ∞ まで伸びているのである（これは重要）。このような正しい絵はコンピューターでは決して作れない。
　　　　右の図は左の図の小部分である。線香花火のような穂先がきれいです。下側にカージオイドの半分の形が見える。 絵は上下対称なので，
　　このカージオイド（1 の領域）は原点を含んでいる。2次関数のマンデルブロー集合でもカージオイドが現れたが，なぜカージオイドが出て
　　くるのだろう。ちょっと考えよう（ [4], p194 参照）。

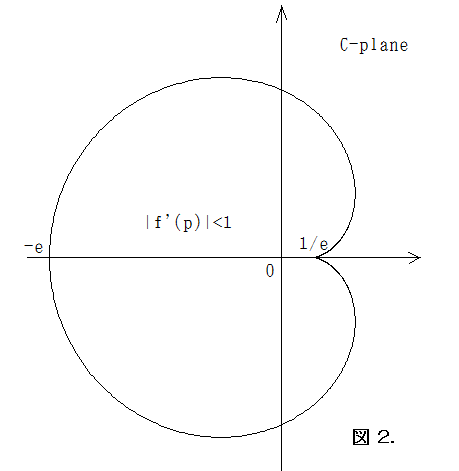　 pを吸引的固定点とすると
　　　　f(p)=c ep=p,　　　f '(p)=c ep=ς ,　　　|ς |<1 　　　　　　　　　　　　　　　　　　　(e.2)
が成り立つ。これは，　　　c =ςe-ς,　　|ς |<1 　　　とかける。この領域の境界の方程式を求めたい，
ので，　　　ς =cosθ +i sinθ 　　とおくと，
　　　c=(cosθ +i sinθ )e-cosθ -i sinθ = … =e-cosθ{cos (θ-sinθ)+i sin(θ-sinθ)} 　　となる。即ちパラメ
ーター表示すると
　　　　　　　　　　x=e-cosθ cos (θ-sinθ),　　y=e-cosθ sin (θ-sinθ).　　　　　　　　　　　　　(e.3)
式(e.3)で表される曲線が左図のカージオイド曲線である。2次関数のときのカージオイド（ [3],p152 参照）
とは方程式が異なる。このように解析的にカージオイドとなることが分っても，“なぜカージオイドなのか”
という問の答にはなっていないね。どうしてでしょうか，不思議だね。

　　　　ここで，パラメーターc を適当に選び，ジュリア集合・ファトゥ集合の絵を描いてみよう。



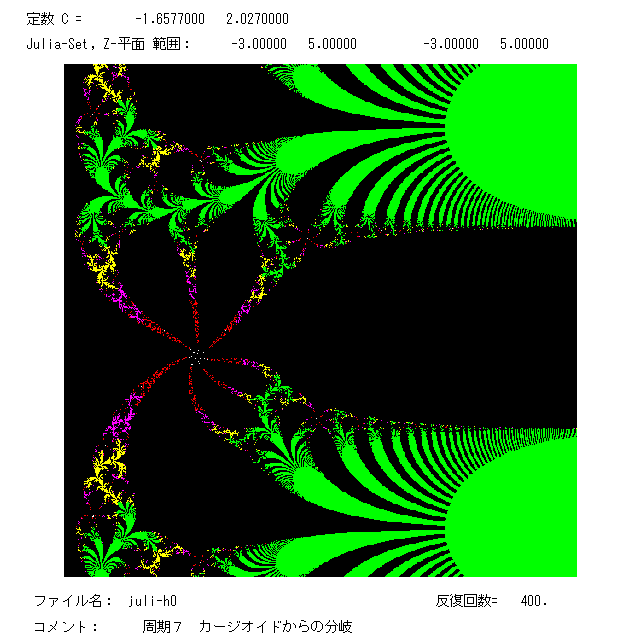
　　　　左の図は，周期7の吸引的周期点をもつ例である。１つの反撥的周期点を中心に黒の七枚の花びら（ファトゥ成分） があり，その中に
　　７つの周期点が入っている。ファトゥ成分は単連結で∞ まで伸びている（この事実は絵では見えない）。緑色のシダ植物の葉っぱのような
　　形は，カントールの花束と呼ばれている。ジュリア集合は黒のファトゥ成分と色の付いている領域 If の境界（フラクタルな曲線）である。
　　超越整関数のジュリア集合は全不連結にはならないことが分っている。
　　　　右の図は，周期40の吸引的周期点をもつ例である。大小，色とりどりのカントールの花束模様がきれいな絵である。 周期40という事実
　　は計算で簡単に確かめられる。２つの絵の見栄えを良くするため，カラーは少し変えた。

　　　　ここで，指数関数がかもしだす典型的な形；カントールの花束の絵を３つ並べよう：


　　　　さて，この絵がなぜ “カントールの花束” と呼ばれているかお気づきでしょうか？　1番左の絵を見ていただきたい。黒の領域（黒の帯）
　　は右へ，赤の領域にどんどん食い込んでいきます。この食い込みは実は無限遠点 ∞ まで行きます。全ての黒い帯が同様に ∞ まで届きます。
　　花びらの先端にある緑の葉の間にも同様の黒い帯があり，これらの帯も赤の領域に割って入りこみ無限遠点まで伸びます。赤の領域からこの
　　ような帯をどんどん抜いていくと，無限個の曲線が残ります。カントールの三進集合の作り方と同じ構造になっているのが分りますか。ただ，
　　この場合は点集合ではなく，曲線の集合です。この曲線の集合がジュリア集合 J です。
このページのトップに戻る 　第1ルームの目次に戻る

E-2. 三角関数ともう1つの指数関数

　　　　ここでは c=a+i b をパラメーターとした三角関数 g(z) ともう一つの指数関数 h(z) のジュリア集合・ファトゥ集合の絵を示す。
　　　　　　　　　　　　　　　g(z)=c sin z 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(e.4)
　　　　　　　　　　　　　　　h(z)=c+2z - ez 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (e.5)
　　正弦関数 g(z) の臨界点は ± (2k+1)π/2 （k は整数），これを写像した臨界値は ± c 。この２つの臨界値の軌道は；
　　　　　　　g(c)= c sin c, 　　　 g2(c)= c sin (c sin c) , 　　… 　および
　　　　　　　g(-c)= c sin (-c)=-c sin c, 　　　 g2(-c)= -c sin (c sin c) , 　…
　　だから，2つの軌道は原点対称である。よって，もし g(z) が吸引的周期軌道を２つもてば，それらは原点対称である。また，異なる周期の
　　吸引的周期点を同時に２つもつことがないことも分る。ジュリア集合・ファトゥ集合の絵を２つのせる。



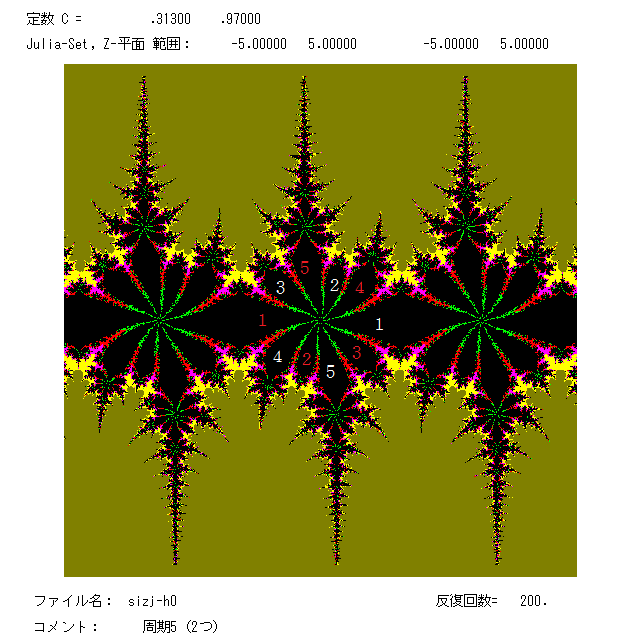
　　　　左の図は，周期5の吸引的周期軌道を２つもつときの絵である。２つの軌道の周期点は，同じ色の番号のついた ファトゥ成分の中に
　　ある。ジュリア集合は黒の領域と色のついた領域の境界の曲線である。塔またはイバラのようにつながった黒の領域が上下に伸びているが，
　　これらは実は無限遠点まで伸びているのである（絵では分らない，定理５，定理６参照）。このイバラやトゲでできたような痛々しい形が
　　正弦関数の特徴のようである。
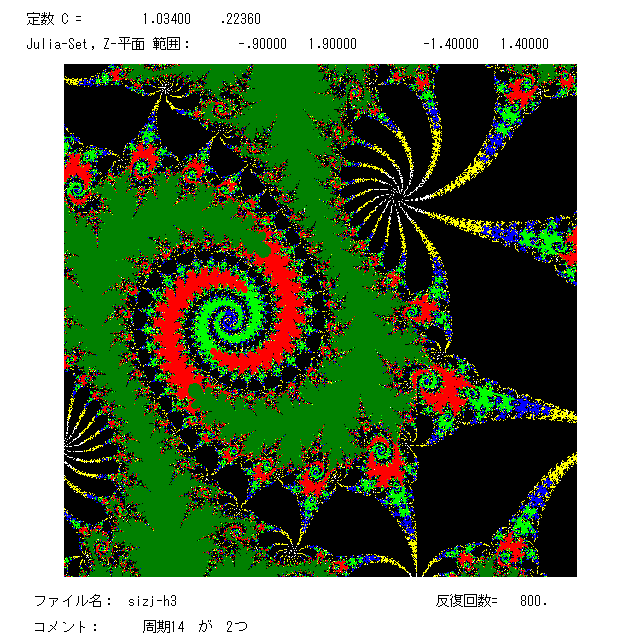
　　　　右の図は，周期14の周期軌道を２つもつときの絵である。原点を含む狭い領域の絵であるが，右上部分の14個の ファトゥ成分の中に
　　１つの周期軌道が入っている。左下の方にもう1つの軌道が入る14個のファトゥ成分があるのだが，隠れていてよく見えない。一番大きな
　　渦の中心が原点，原点は反撥的固定点である。

　　　　さて，h(z)= c+2z - ez のジュリア集合・ファトゥ集合を考える。この関数の特徴は，反復計算で Re(z) がいったん負になると，
　　Re(h(z)) < Re(z)　が成りたつので，左半平面で ∞ に向かうことなる。この領域が　Baker 領域（周期1，[1] p.67 参照）ですね。また，
　　臨界点は　log 2　のみ，特異値はないので，吸引的周期軌道はあっても１つである。２つのジュリア集合・ファトゥ集合の絵をのせる。



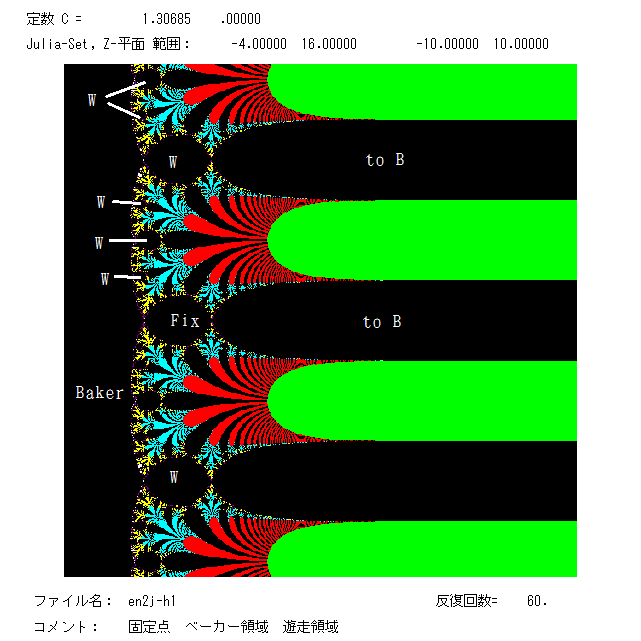
　　　　左の図は，c= 2 - log 2 のときのジュリア集合・ファトゥ集合の図である。このケースは，log 2 が吸引的固定点かつ 臨界点である。
　　log 2 の逆像は存在しないことが確かめられるので，log 2 の安定領域は，直接鉢 A(log 2) のみである（Fix とかいてあるファトゥ成分）。
　　絵のカラーがついてる部分は数列が右半平面で ∞ に近づく領域である。A(log 2) 以外の黒の領域は，2種類ある。１つは W とかいてある
　　遊走領域（wandering domains）である。ある遊走領域から出発した軌道は別の遊走領域に写像され，遊走領域を渡り歩いて ∞ に発散す
　　る。例えば，　　log 2+2π i　→　log 2+4π i　→　log 2+8π i　→　… 　→　∞　　となる。 この遊走領域はほぼ楕円形で，Baker 領域
　　に接するように大きいものから小さいものまで無限個ある。もう１種類の黒の領域は，Baker 領域に落ち込んでしまう初期値の集合である。
　　これらのファトゥ成分は，すべて単連結で非有界のようである。
　　　　右の図は，c=1.55+.623 i　のもので，周期3 の吸引的周期点をもつ。図の中央付近に周期3 の ファトゥ成分（ラビットの形）がある。
　　1, 2, 3 の番号は，そこに3つの周期点があることを示す。左の黒の領域（Re(z) ≤ - 1.75 を含むあたり）はBeker 領域。Baker 領域に隣接
　　する小さなラビットの形がいくつか見えるが，これらは遊走領域である。全体的な力学的構造は左の絵に似ている。

このページのトップに戻る 　第1ルームの目次に戻る

E-S. すてきな絵； wonderful pictures； las pinturas bonitas

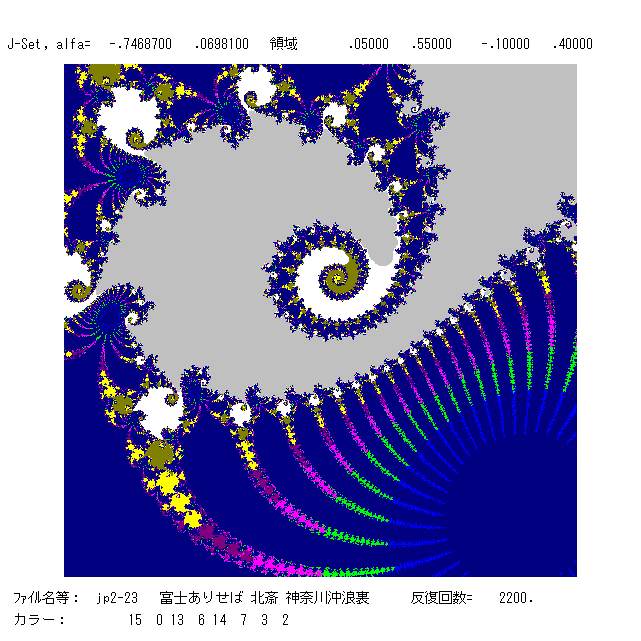
　　　　ここでは，面白い絵，素敵な絵，不思議な絵などをとりあげます。
　　1段目）　左：　3つ目の絵（jp2-ho1）と同じだが，少しずらして色をかえた。富士山と船があれば，北斎の有名な “神奈川沖浪裏” に似て
　　　　　　　　　いませんか？
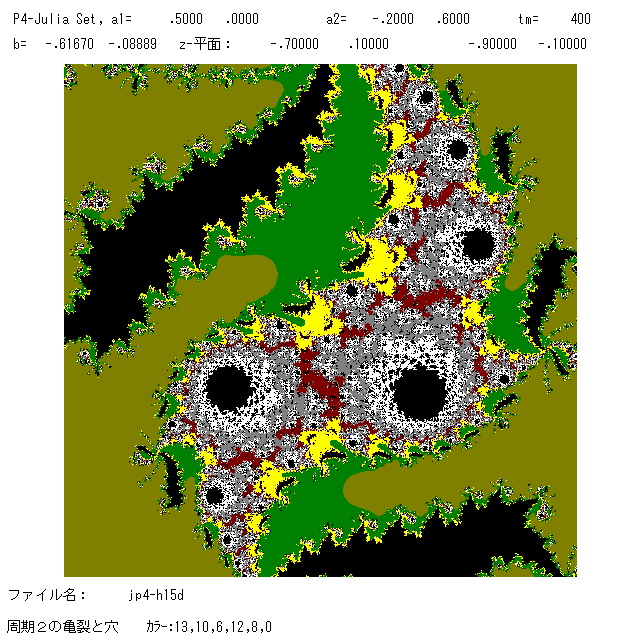
　　　　　　  右：　4次関数の絵，O+(a2) は周期2に収束。O+(a1), O+(a3) は発散。黒のホールは実際には存在しないかも（fake holes？）。
　　2段目）　左：　指数関数(e.1) のもの。なめらかな流線形の曲線がいいね。
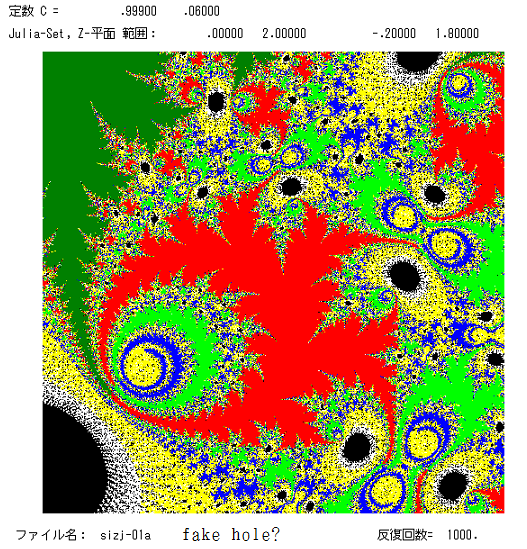
　　　　　　  右：　正弦関数(e.4) のもの。黒の部分は fake holes かな。





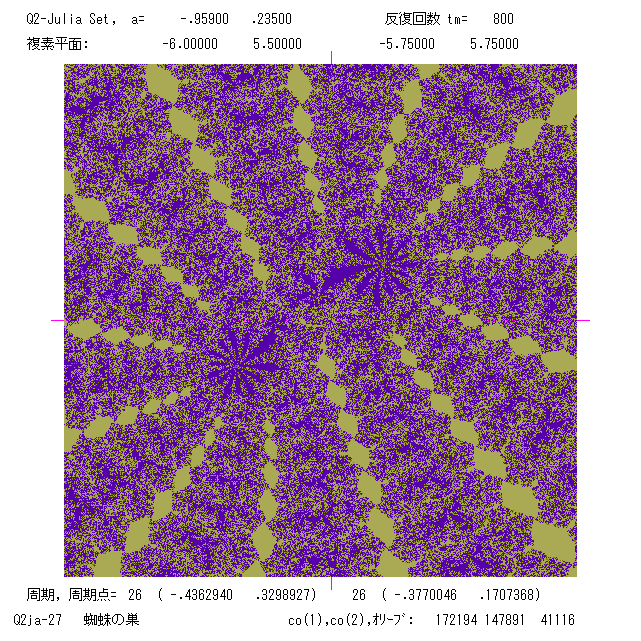
　　　　次の2枚の絵は，関数 Q(z) （次節）のパラメーターa が点 E, F のときのジュリア集合。プログラムは Q2jb.BAS による。



　　またここで，関数 Q(z) で少し面白いものができたので，のせます。左図は周期26のコラボレーションです。 A0 と B1 の分岐がぶつかって
　　いる所からパラメーターa を選んだよ（蜘蛛の巣みたい）。右図は 周期4の周期軌道を1つだけもつときの絵です。比較的大きな４つのファ
　　トゥ成分の結節点が原点ですが，ちょっとボケています。しかし，細胞のような形が，まあ綺麗ですかね。




　　　再び　g(z)=c sin z　 のジュリア集合の絵を2つのせます。左図は周期7の吸引的周期軌道を二つ もつ場合で，痛々しいトゲトゲの紋様は
　 正弦関数らしくない形で，けっこう好きですね。右図は，ジュリア集合がカントール集合 だと思われるものです。黒の穴に見える領域は，
　たぶん fake hole です。トゲトゲな形はやはり随所に残っています。




　　さて，このホームページでは扱わなかった有理関数
　　　　　　　　　　　　　　　　　　　R n(z)= zn-1(1-a z)/(z-a)　　　　　　　( 0< a< 1, n=3, 4 ) 　　　　　　　　　　　　　　　(r. 0)　
　のジュリア集合の絵を２つのせる。この関数についての性質や定理，プログラムについては文献 [3] を参照せよ。絵はx 軸対称で単純な繰り返
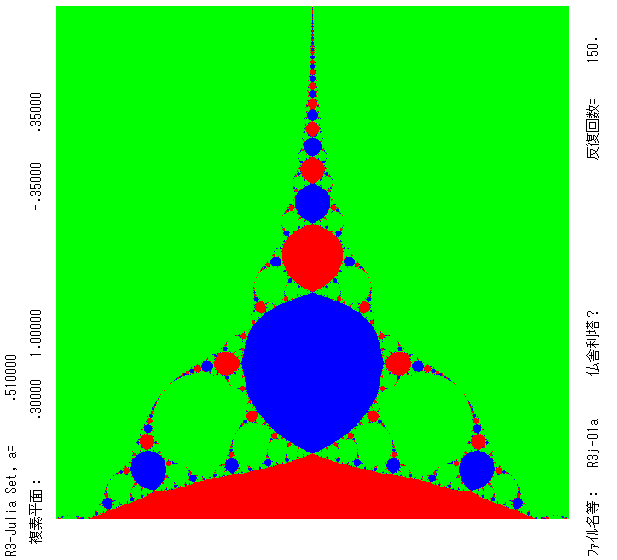
　しパターンからなるが，簡素な美しさがある。左図は　n=3, a=0.51 のもの。0 と ∞ が吸引的固定点（これらに収束する ファトゥ成分は赤と
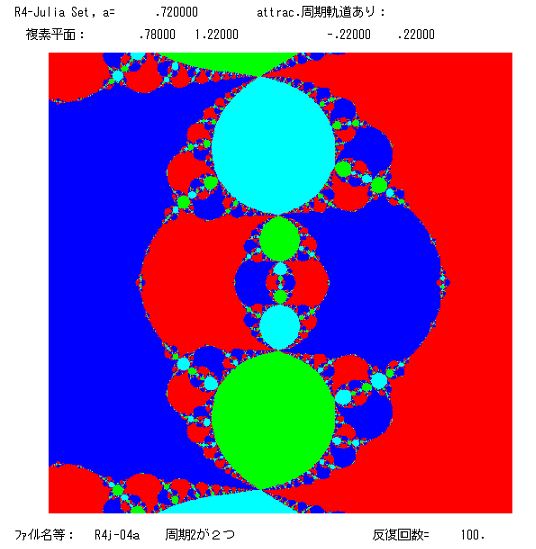
　青），緑は周期2の吸引的周期点に近づくファトゥ成分。図は90°回転してある。右図は n=4, a=0.72 のもの，0 と ∞ が吸引的固定点（これ
　らに収束するファトゥ成分は赤と青）。緑と空色のファトゥ成分は，それぞれ異なる周期2の周期点に近づく領域である。



　　ここで，文献[3] の正誤表を示します。既に本を購入した方，これから購入する方は参考にして下さい。公表が遅くなったことお詫びします。
　 　　
正誤表
　ページ，　行　 　　　　誤　 　　　　正　
　p.26, 　下から5行目   　 　 -3/2± (√11/2)    　　 -3/2± (√11/2) i    　
　 p.139, 　9 行目　 　 3)　　| λ | =1    　 　 4)　　| λ | =1    　
　p.147,　3行目　　… , .8, 100     　… , .8, 200     (注1)
　p.147,　9行目　　n1= 400     　n1= 600     (注1)
　p.151,　3行目　　f(z)= x2+α     　f(z)= z2+α    
　p.154,　図(c)の下　　[-1, 0.6 ]× [0, 0.4]     　[-1, - 0.6 ]× [0, 0.4]    
　　　　　　　　　　　　　　　　（注1） この後にある絵を描くプログラムの全てを，これと同様に修正して下さい。
　　　　　　　　　　　　　　　　　　　（例えば，Manp2.BAS, Julia3.BAS など）

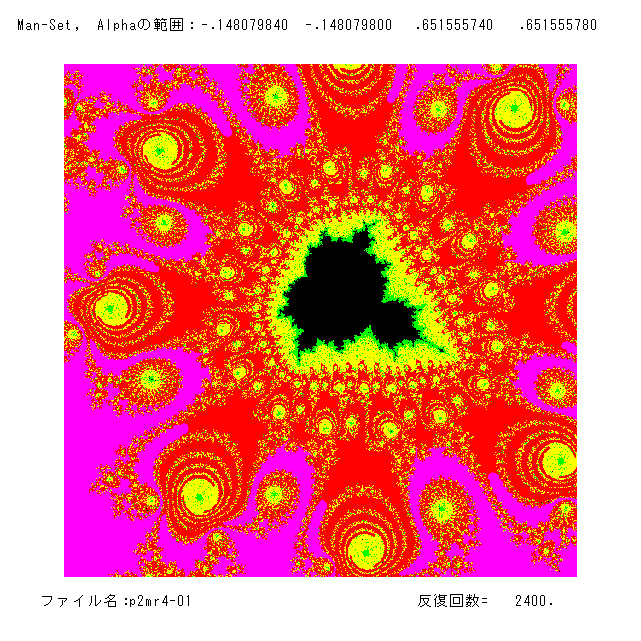
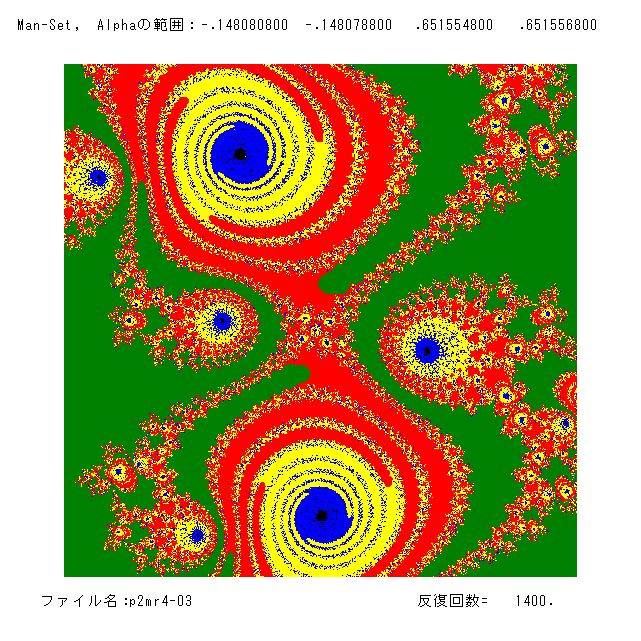
　　（9月16日 '22 記）ここでは，2次関数 (p.1)　f(z)=z2+α　 のマンデルブロー集合（元祖マンデルブロー集合）の，微小部分でちょっときれいな絵
　　（昔，数学者やマニアの方々が好んで描いた騒がれたパート）を2枚のっけます。α平面の範囲は複素平面上の以下の2つです。
　　　　(左）[-.14807984, -.1480798]×[.65155574, .65155578]　　　　（右）[-.1480808, -.1480788]×[.6515548, .6515568]
　　こういう絵は，カラーを変えるとすごく見栄えが良くなったりしますよね。プログラムは，文献[3]にありますので（上の正誤表の注意の部分に注意），暇が
　　ありましたら，カラーや反復回数を変えて，やってみてください。（そんな暇ないかな？）


　 このページのトップに戻る 　第1ルームの目次に戻る

R-ex. ある有理関数

　　　　ここでは，１つのパラメーター a をもつ次の有理関数をとりあげる。

　　　　　　　　　　　　　　　　　　　Q(z)= z/(z2- az+a)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (r.1)

　　ここに，　　Q(z)=z　　⇔　　z3 - az2 + (a -1)z=0　　⇔　　z(z -1){z - (a -1)}=0　　より， 固定点は　0,　1,　a -1 ．
　　微分は　　　　　　　　　　　　　　Q'(z)= (a - z2)/(z2- az+a)2　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(r.2)
　　なので，　　　　　　　　 　　Q'(0)=1/a,　　　Q'(1)=a -1,　　　Q'(a -1)= - a2+3a -1.　　　　　　　　　　　　　　　　　　(r.3)
　　また，　Q2(z)=z　より，周期2の周期点は　　
　　　　　　　　　　　　　　　　　 q 1={a+1+ √(a2- 2a -3)}/2,　　q 2={a+1 - √(a2- 2a -3)}/2. 　　　　　　　　　　　　　　　(r.4)
　　これらの微分係数は　　　　　　　　　(Q2)'(q i)= - (a3- 2a2- 3a -1),　　 ( i=1, 2 ).　 　　　　　　　　　　　　　　　　　　　 (r.5)
　　　　３つの固定点と周期2の周期軌道が吸引的となるa-平面の領域を次のように定義する。
　　　　　　　　　　　　　　　　　　　　A0={　a　|　　|a|>1　},
　　　　　　　　　　　　　　　　　　　　A1={　a　|　　|a -1| <1　},
　　　　　　　　　　　　　　　　　　　　A2={　a　|　　|a2 -3a +1| <1　},
　　　　　　　　　　　　　　　　　　　　B1={　a　|　　|a3 -2a2 -3a -1| <1　}.
　　Q(z) の臨界点（critical points）は，±√a なので，臨界点の軌道が発散しないということで，マンデルブロー集合（おとといのジョーの勝手
　　な定義かも?）を定義する。
　　　　　　　　　　　　　　　　　　　M={ 　a　|　　O+(±√a)　 —⁄→ ∞　　}.

　　　　さて，領域　A i (i=0,1,2) と B1 を示したものが下の図３，領域 A2 と B1 は２つの領域から成ることに 注意されたい。
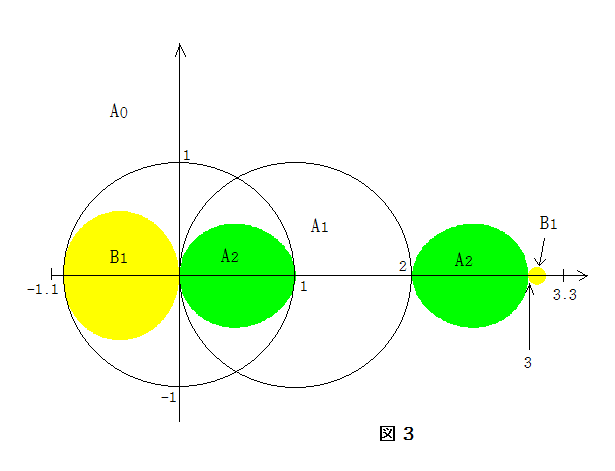　単位円の内部で A i (i=1,2) と B1 以外の領域がちょっと 面白いところでしょうか。Q(z)
は2次の有理関数なので吸引的周期軌道（固定点を含む）は多くても2つです。マンデルブ
ロー集合作成では，軌道 O+(±√a) の最終状態で色付けします。
　 　　
マンデルブロー集合
　軌道状態 　O+(-√a) 収束     O+(-√a) 収束しない  
　O+(√a) 収束　 　　　　黒 　　　　　赤
 O+(√a) 収束しない   　　　　緑 　　　　　黄

臨界点の軌道 O+(±√a) が収束しない（カオテックである）ということの判断は，簡単では
ない。ここでは，カオテックの判断を次のように設定した（これはマンデルブロー自身のア
イデアと聞いています）。


　　　　判定基準 (H):　　　　∃N と定数 C に対して，　|　Qn(±√a)　| > C 　( n≥ N)　が成り立ったとき。
　　N と C の選び方は，反復計算の経験に頼っている。ここでは，N は10 から 200 の間の適当な値，C は 3.5 から 4 の間の値を選んだ。絵
　　の下にこの値があるので参考にして下さい。また，臨界点の軌道が収束したという判定は，“反復の限界値 tm まで計算された” ときとした。
　　という訳で，マンデルブロー集合を表すカラーの図は 100% 正確なものではない（大まかな図と言っていいが，間違いではない）。下の２
　　つの図は，黒の領域がマンデルブロー集合である。記入されている数字は，その領域が持つ吸引的周期軌道の周期である。４つの領域
　　A i (i=0,1,2), B1 のどの分岐かが分るように，カラーの数字（それぞれ，白，黄，水色，ピンク）を用いた。


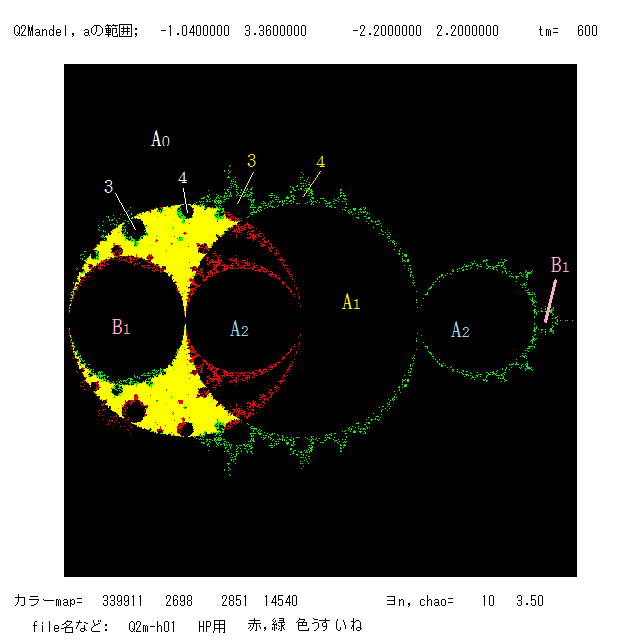
　　　　左の図は，マンデルブロー集合の全体図；おきあがりこぼし（起き上がり小法師，おきゃがりこぼし）が横になっている図かな。 右図
　　は単位円内を拡大したものである。領域　A i , B1 からの分岐の様子がよく見える。単位円周上から黄色 の部分に食い込んでいる雪だるま，
　　および単位円内部に食い込んでいる赤い部分の雪だるまは，A0 からの分岐である。領域 B1 の上方と下方に，赤と緑の霞のような模様が見え
　　るが，ここは興味深い。しかし，赤と緑の点々は，正確ではないので，100% 信用しないことです。 また，A0 と A1 が交差している1点
　　 (1/2, √3/2) の近傍も興味深い。これらの部分を拡大したのが次の図である。


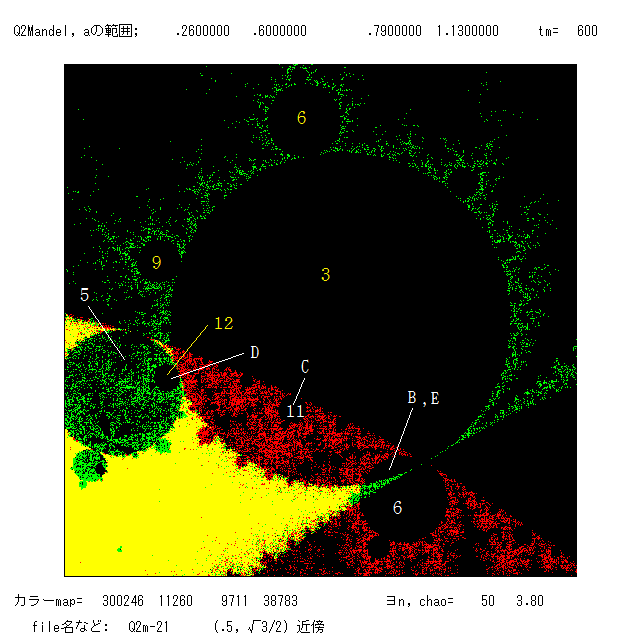
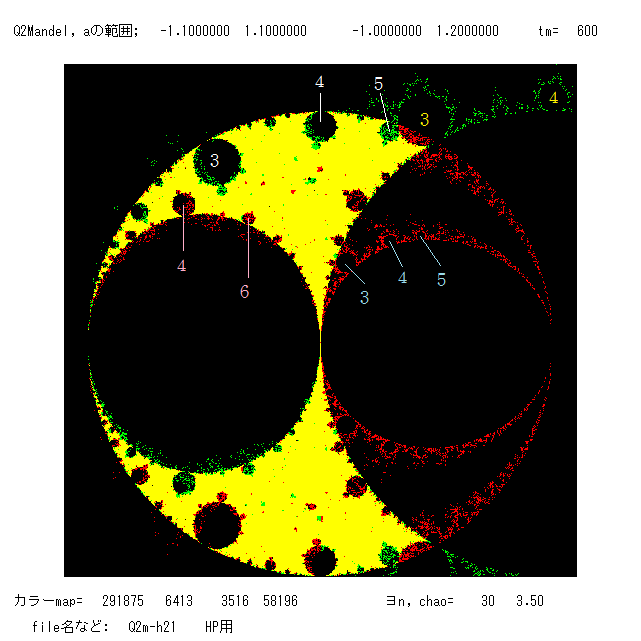
　　　　左図の B1 からの分岐の1番大きな雪だるま（の胴体部分;以下同様）は周期4の領域， その右の2番目に大きな雪だるまは周期6の領域，
　　この２つの雪だるまの間（B1内）に，赤く縁どられた雪だるまが見える。これは O+(-√a) が落ち込む周期4 の領域である。 即ち，ここから
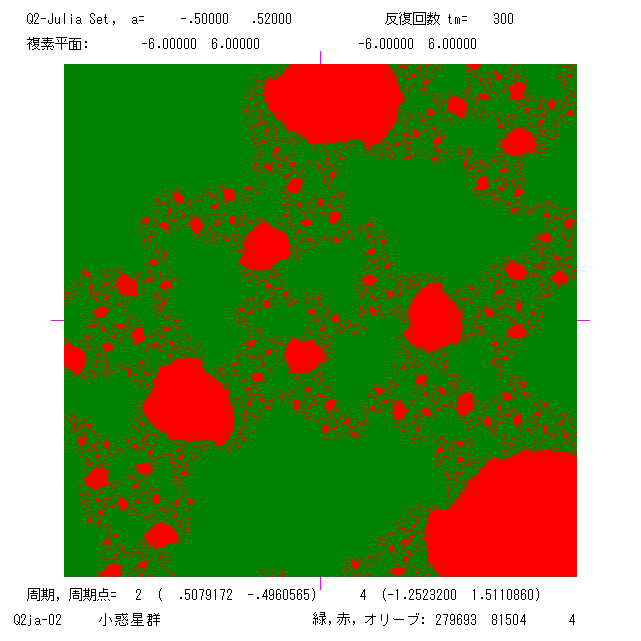
　　パラメーター a を選べば，吸引的な周期2と周期4が同時に存在する（ジュリア集合の絵 Q2ja-02, Q2jb-te1 参照；A, F）。この図の上部 A0
　　からぶら下がっている1番大きな雪だるまは，周期3の領域である。また，この図には Mと繋がっているのかいないのか分らない小さな雪だる
　　ま（黒および赤や緑のもの）が10個ほど見える。B1 から分岐した周期6 の領域に突き刺さった雪だるま（一部緑色になっている）も見える。
　　Mの構造は私にはよく分らない。
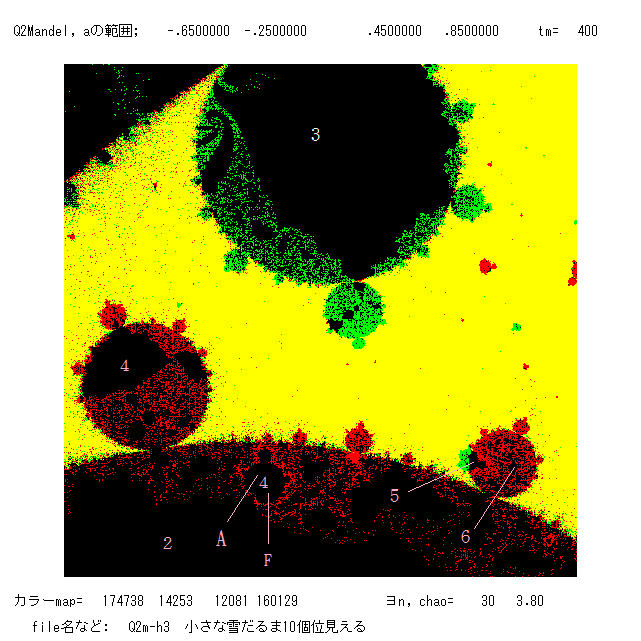
　　右図では，1点 (1/2, √3/2) の上部に A1 から分岐した周期3の雪だるま（緑で縁どられている）と 下方に赤で縁どられたやや小さい A0 から
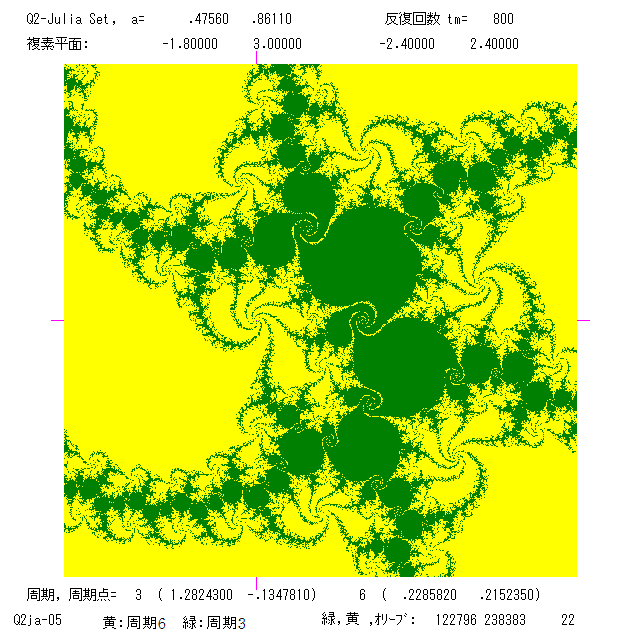
　　分岐した周期6の雪だるまが交差している。この交差した部分から aを選べば，吸引的な周期3と周期6を同時にもつ絵が得られる（ジュリア集
　　合の絵 Q2ja-05, Q2jb-12 参照; B, E ）。ここで，吸引的周期軌道を２つもつジュリア集合の絵（A と B ）をのせる。色の境界がジュリア
　　集合で，これらは連結である。プログラムは Q2ja.BAS です。


　　　　上の2つの絵は2色しか使ってないので，単純な良さがある。しかし，もっと見栄えを良くしたいので，吸引的周期軌道の周期の数だけの
　　色を使うことにする。周期k の周期軌道を {pi}　(i=1,2, ... ,k)　として，収束判定を
　　　　　　　　　　　　　　　　　　　| Qn(z0) - p i |< 0.01　　　( i=1,2, ... ,k )　　　　　　　　　　　　　　　　　　　　　　　　(r.6)
　　で行い，初期値 z0 に i に依存した色をつける（全部で k 色）。1つの周期軌道には同系色の色を使った。用意したのは， ［緑っぽい色］，
　　［赤っぽい色］，［黄色っぽい色］，［青っぽい色］ の4種類です。使っている2種類の色の境界がジュリア集合です。本当は，周期 k の各
　　ファトゥ成分に異なる色をつけ，それらの逆成分にも同じ色を付けたいのであるが，これを実現するアルゴリズムはちょっと分らない。
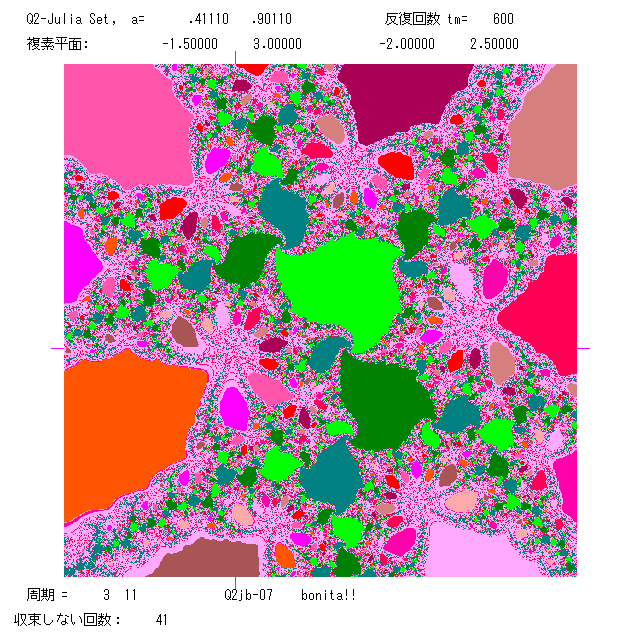
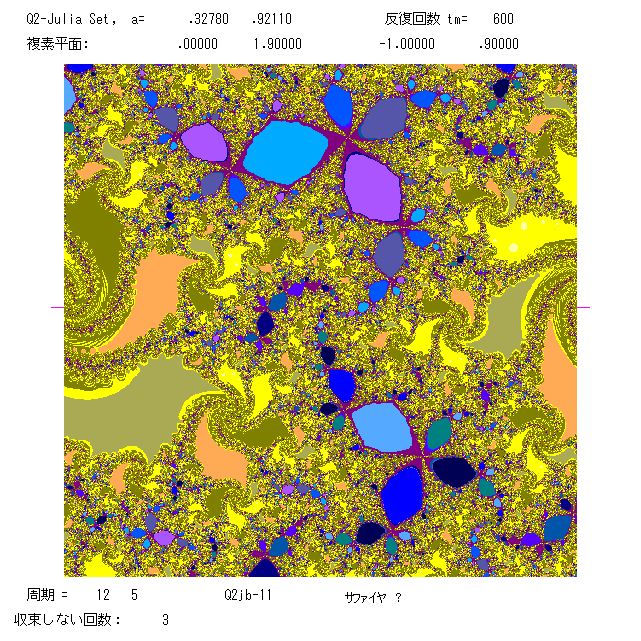
　　　　下の4枚の絵は，上段が a=0.4111+ 0.9011 i （C; 周期3 と 11）, 下段が a=0.3278+0.9211 i （D; 周期12 と周期5）のものである。
　　右の絵は，左の小部分。下段では，色彩を変えた。プログラムは Q2jb.BAS です。




　　　　さて，吸引的周期軌道が1つの場合，ジュリア集合やファトゥ集合の絵をどうやって描いたらいいでしょうか。例えば，
　　　　　　1)　a=1+2i ∈A0　のとき，原点 O のみが吸引的固定点，
　　　　　　2)　a=0.5+0.7i ∈A1 (かつ a∉A0, a∉A2)　のとき，z=1 のみが吸引的固定点，
　　　　　　3)　a=- 0.5+0.4i (Re(z)<0 の B1 の内部)　のとき，周期2の周期軌道が１つ，
　　　　　　4)　a=0.95i　のとき(A0 の分岐)，周期4の周期軌道が1つ，
　　などのケースです。ジュリア集合は空ではないので，カントール集合か連結集合（有界または非有界な曲線）です。1), 2) のケースは，ただ
　　1つのファトゥ成分は無限連結で，ジュリア集合 J はカントール集合なので，ファトゥ成分を絵にするのは困難である。 しかし，z∈J のとき，
　　　　　　　　　　　　　　　　　　　　　　　　　　J=closure( Un≥0 Q-n(z) ) 　　　　　　　　　　　　　　　　　　　　　　　　　 (r.7)
　　なので，反撥的周期点の逆像を次々にプロットすることでジュリア集合を構成するという方法がある。このやり方で作った図も後でのせるが，
　　満足できるようなものは作れない。というのは，J が複素数平面 C 上で非有界のとき，パソコンでは無限個の逆像は 作れないからである。
　　集合 J が有界ならば，本物の J に近い図は作ることができる。
　　　　3), 4) の場合はファトゥ成分の色付けは可能だろうか。吸引的周期軌道は１つしかないのだが，プログラム Q2jb.BAS が使える。固定点
　　0,1 または a-1 を吸引的固定点であると考えて，これをダミーとして利用する。即ち，１つの吸引的固定点（ダミー）と，もう1つ吸引的周期
　　軌道をもつとしてプログラム Q2jb.BAS を使う。吸引的周期軌道のファトゥ成分は，［緑っぽい色］,［赤っぽい色］, … のうちの1種類の色
　　で描かれる。1つのファトゥ成分が1色とは限らないので注意すべし。下に絵を２つのせる。左図は 　a=- 0.5982+0.6062i のもので，周期4
　　の軌道を１つもつ。領域 B1 からの分岐である。千代紙のような模様がかわいい。右図は 　a=0.1419+0.6062i のもので，周期5の軌道を1つ
　　もつ。領域 A1 からの分岐である（渓谷などでしぶとく生える低木の若葉と古葉に見えませんか）。



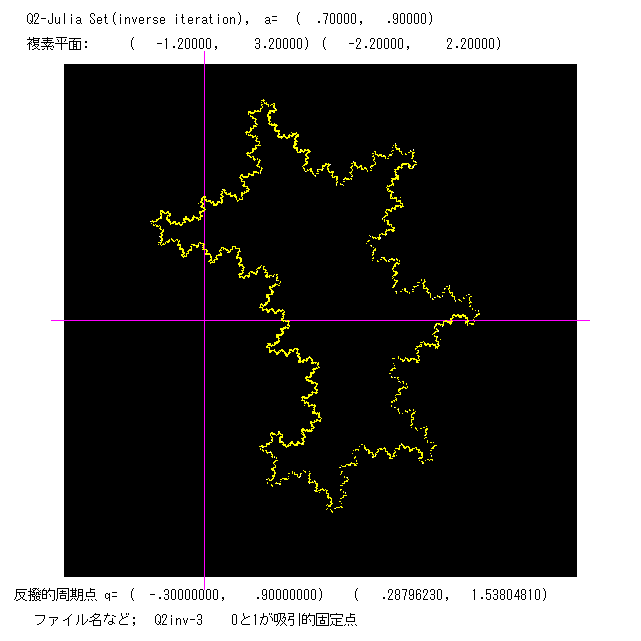
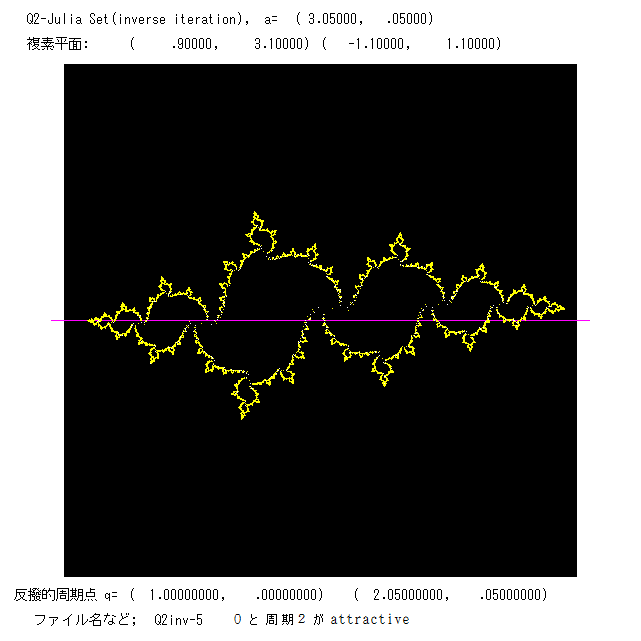
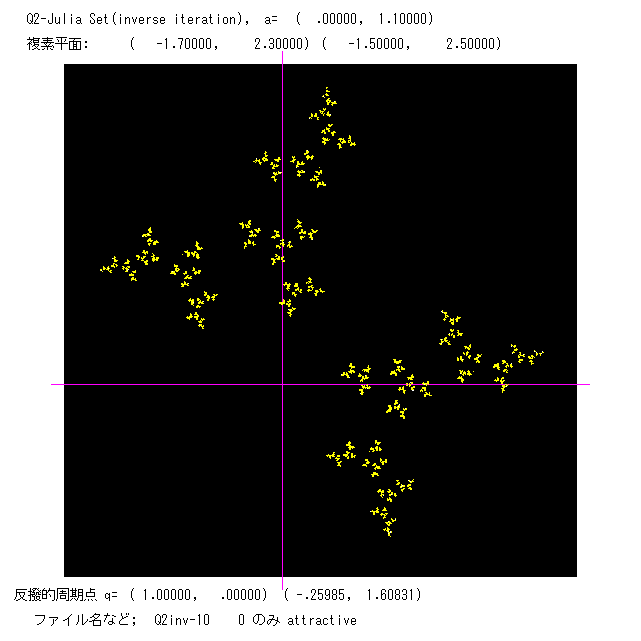
　　　　最後に，反撥的周期点の逆像を次々に作っていく方法で描いたジュリア集合の図をのせる。ジュリア集合J がある一定の領域の中で 有界
　　のとき，まあまあ見られる図を描くことができる。J が複素数平面C 全域に広がっている場合は，まともな絵は 得られません。プログラムは
　　 Q2inv.BAS です。３つの図をのせます。左の２つは，吸引的周期軌道を２つ，右の図は 0 のみが吸引的固定点で J はカントール集合。


このページのトップに戻る 　第1ルームの目次に戻る

F-o. 公開ファイル

　　　　絵を作成した 十進BASIC のプログラムファイルを公開します。文献[3]で紹介したプログラムはここにはありません。最初に，
　　プログラムのダウンロードがあるので，あなたのパソコンで十進BASICが使えるように準備しておいて下さい。このソフトは，
　　フリーソフトで誰でも自由に使うことができます。
　　十進BASICのホームページ−Vector 　へリンク 　　　　絵を描くプログラムでは，最初に “テストか本番か” を聞いてくるので，テストを選ぶことを勧めます。本番はテストの9倍の時間がかか
　　ります。ダウンロードは，面倒ですが1つずつ行って下さい。また，表示されたファイルのセーブ（自分のパソコンへのセーブ）も自分でやっ
　　て下さい。
　　【注意】ダウンロードされたBASICプログラムの拡張子は txt （テキストファイル）になっています。これは，本来の十進BASICプログラム
　　　　　　の拡張子 BAS とは異なります。従って，プログラムを走らせる時は，テキストファイルを十進BASIC用のファイル（拡張子 BAS の
　　　　　　もの）に変換し直してから使って下さい。

　　1)　p4iteration.BAS　 ........ 4次多項式 (p.2) で作られる数列の計算。初期値を入力し，n1 と n2 の間の数列を表示する。 　　2)　 manp4a.BAS　 　........ 4次多項式 (p.2) の a1, a2 を固定して，b 平面でマンデルブロー集合 を描く。入力は，a1 と a2 の値，
　　　　　　　　　　　　　　　　 b 平面上の四角形（正方形がよい）領域と数列の反復回数（tm）。反復回数は，表示領域が小さい時は
　　　　　　　　　　　　　　　 　やや大きめにする。 　　3)　 manp4b.BAS　 　........ 4次多項式 (p.2) の a1, b を固定して，a2 平面で マンデルブロー集合を描く。入力は，a1 と b の値，
　　　　　　　　　　　　　　　 　a2 平面上の正方形領域と反復回数。 　　4)　 julia4.BAS　　　 ........ 4次多項式 (p.2) の a1, a2, b を固定して z 平面上でジュリア集合・ ファトゥ集合を描く。入力は，a1，
　　　　　　　　　　　　　　　　a2, b の3つの値と，z 平面の正方形領域，および反復回数。 　　5)　 mp4a-16.BAS　　........ manp4a と同じ図を16枚いっぺんにつくる。下図のように１つ１つは小さな図である。a1 を固定して，
　　　　　　　　　　　　　　　　16個の a2 に対して b 平面上にマンデルブロー集合を描く。a2 の値を連続的に動かすことで，マンデル
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　ブロー集合の変化を見ることができる。面白い絵をみつ
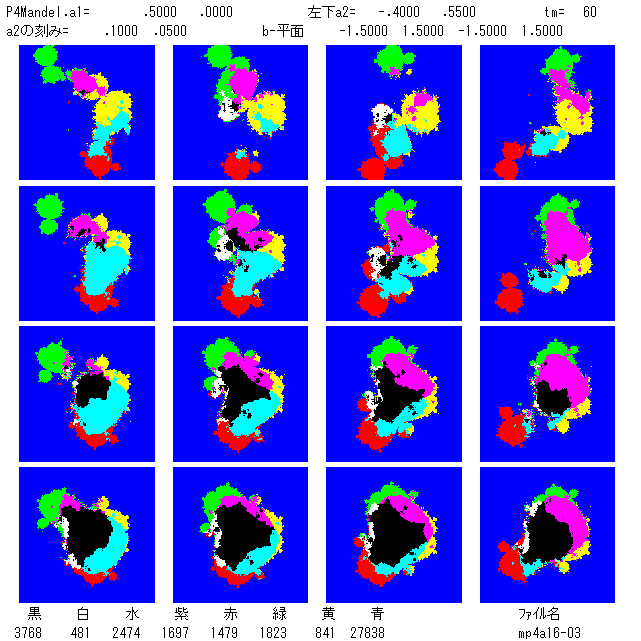けることもできる。入力は， a1 と，左下に位置する図
（これを (1,1)成分と呼ぶ）の a2 の値。(1,1)成分と
右隣りの (2,1)成分との差が Δa2r，(1,1)成分と上の(1,2)
成分との差が Δa2i。この２つの値（横と縦の刻み幅）も入
力する。即ち，16枚の図の横方向の差が Δa2r，縦方向の
差が Δa2i である。参考のために，(2,2)成分の図に対して
は，色付けしたカラーのドット数を，図の下方に表示して
ある。これで色付けされた各領域の大きさが分る。(3,2)
成分の図が，4次関数の所で取りあげた牙のある絵である。

　左の図では，a2 の値に関して，横方向（実軸）の刻みは
0.1，縦方向（虚軸）の刻みは 0.05 になっている。また，
反復回数の入力は最後であるが，100 以下で十分です。

6)　 mp4b-16.BAS　　........　manp4b と同じ図を16枚
　　　　描く。a1 を固定して，16個の b に対して a2 平面
　　　　上にマンデルブロー集合を描く。基本的には左の図
　　　　と同じである。
7)　 Exziteration.BAS　 ........　指数関数(e.1) の数列の
　　　　計算。初期値を与え，n1 と n2 の間の数列を表示
　　　　する。

　　8)　 ExzMan.BAS　 ........　指数関数(e.1) のマンデルブロー集合の絵を c 平面上に描く。c を与え，零の軌道 O+(0) が発散するか否
　　　　　　　　　　　　　　　　かで色付けする。発散のとき黒以外の色をつけ，発散しないとき黒とする。発散は　|f(zn)|> 1025 または
　　　　　　　　　　　　　　　　Re(zn) > 60 で判定。この基準はかなり甘い基準である。というのは，10進BASICでは exp(230) は “桁
　　　　　　　　　　　　　　　　あふれ” と判定されそこでプログラムが止まってしまいます。この事態を避けるため，かなり小さめの値で
　　　　　　　　　　　　　　　　発散の判定をしている。基準は使用するコンピューターの性能（ exp(x) の計算限界）によって作られる
　　　　　　　　　　　　　　　　べきものでしょう。
　　9)　 ExzJulia.BAS　 ........　指数関数(e.1) のジュリア集合・ファトゥ集合を描く。初期値 z0 を与え， この軌道 O+(z0) が発散するか
　　　　　　　　　　　　　　　　しないかを調べ，発散のとき初期値 z0 に色をつける。発散しないときは黒。反復回数の限界値（tm），c
　　　　　　　　　　　　　　　　の値，計算するz平面の領域（正方形）を input する。発散の判定はプログラム 8) と同様。
　　10)　 Siziteration.BAS ....... 正弦関数(e.4)の数列を計算。初期値を与え，n1 と n2 の間の 数列を表示する。
このページのトップに戻る
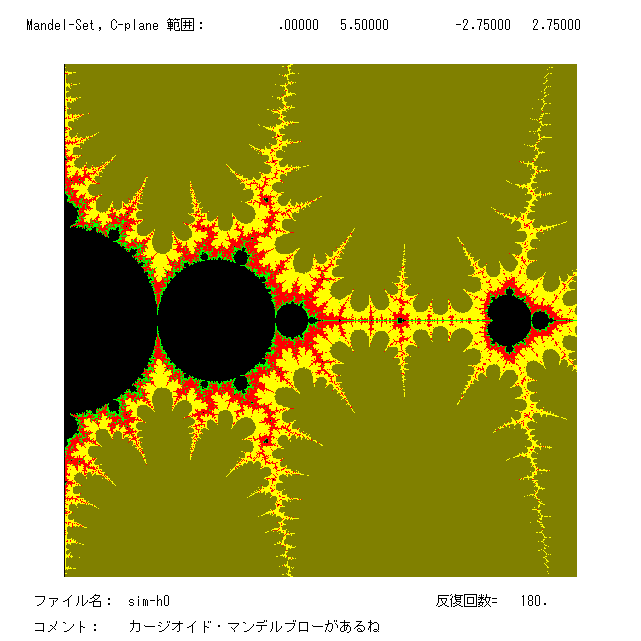
　　11)　 SizMan.BAS　 ........　正弦関数(e.4) のマンデルブロー集合を描く。これがないと，いきなりジュリア集合の絵 を描くことは困難。
　　　　　　　　　　　　　　　　方程式(e.4) の臨界値は ±π/2 であるが，π/2 の軌道のみを追いかければよい。なぜならば，sin z は原点
　　　　　　　　　　　　　　　　対称だからである。軌道 O+(π/2) が発散か否かで絵を描く。発散のとき，パラメーター c に黒以外の色を
　　　　　　　　　　　　　　　　つけ，発散しないとき黒とする。左下に，マンデルブロー集合の図をのせた。右半平面の 絵であるが，左半
　　　　　　　　　　　　　　　　平面は原点対称なので省いた。方程式(e.4) のジュリア集合の図 sizj-h0 はどこからパラメーター c を選ん
　　　　　　　　　　　　　　　　だのかあてて見て下さい。右図は方程式(e.5) のマンデルブロー集合の図。 ついでだからここに並べた。


　　12)　 SizJulia.BAS　 ........ 正弦関数(e.4) のジュリア集合・ファトゥ集合を描く。初期値 z0 を与えて， 軌道 O+(z0) が発散するか否か
　　　　　　　　　　　　　　　 を調べる。発散のとき z0 に黒以外の色を塗る。発散しないとき黒とする。発散は |Re(zn)|>60 or
　　　　　　　　　　　　　　　|Im(zn)|>60 で判定。この関数では，吸引的周期軌道が１つだったり，2つ（同じ周期のもの）だったりする。
　　　　　　　　　　　　　　　この違いはどうして起こるか？答えは出ますかね。
　　13) 　En2iteration.BAS ..... 方程式(e.5) の反復計算。初期値を与え，n1 と n2 の間の 数列を表示する。
　　14)　 En2Man.BAS ........ 方程式(e.5) のマンデルブロー集合を描く。c を与えて臨界点 log 2 の軌道が 発散するか否かを調べる。 発散
　　　　　　　　　　　　　　　のとき，黒以外の色をつけ，発散しないとき黒とする。11) であげた右図が，このマンデルブロー集合です。
　　　　　　　　　　　　　　　またしても，カージオイドと雪だるまが出てきました。このカージオイドの方程式は何でしょう？ 答えをかく
　　　　　　　　　　　　　　　ので，読者諸君が導いて下さい。パラメーター表示関数で次のようになります：
　　　　　　　　　　　　　　　　　　x = 2 - cos θ - log (5 - 4 cos θ)1/2,　 y = - sin θ + tan - 1( sin θ/(2 - cos θ) ).
　　15)　 En2Julia.BAS ........ 方程式(e.5) のジュリア集合・ファトゥ集合を描く。初期値 z0 を与えて， 軌道 O+(z0) が発散するか否かを
　　　　　　　　　　　　　　　調べ，発散のとき z0 に色をつける。発散しないときは黒。発散は Re(zn)>60 で判定。左半平面にある Baker
　　　　　　　　　　　　　　　領域は，チェックしない。
　　16)　 Q2iteration.BAS ........ 方程式(r.1) の数列を計算し複素数平面にプロットする。入力は，パラメーターa の 実部と虚部，表示する
　　　　　　　　　　　　　　　複素数平面の四角形，反復計算の初期値（実部と虚部 x0, y0 ），反復回数tm（収束を確認する時は 2000 から
　　　　　　　　　　　　　　　3000 位がよい）です。数列は最初から最後までが３等分され，緑，黄，赤の色がつけられます。初期値として，
　　　　　　　　　　　　　　　±√a を使う場合は，zroot.BAS で √a をあらかじめ計算して書きとめておくこと。
　　17)　 Q2ma.BAS ........ 方程式(r.1) のマンデルブロー集合を描く。最初に，∃N（プログラムでは小文字のnを使っている） と定数C
　　　　　　　　　　　　　（プログラムではchao を使っている）を入力する。このプログラムもテストか本番かを聞いてくるので，初回は
　　　　　　　　　　　　　テストを選ぶのがよい。反復回数tm の値は∃N の値に依存して決めるのがよい（表示した絵を参考にして下さい）。
　　　　　　　　　　　　　絵を表示するパラメーターa の四角形は，自分で適当に決めて下さい。
　　18)　 Q2ja.BAS ........ 方程式(r.1) のジュリア集合を描く（ジュリア集合は異なる色の境界；普通はギザギザした曲線）。 このプログラ
　　　　　　　　　　　　　ムは吸引的周期軌道（固定点を含む）を２つ持つときの絵である。従って，２つの周期軌道の周期（固定点の場合
　　　　　　　　　　　　　は１）と周期点の１つを入力すること。周期点も，あらかじめプログラムQ2iteration で計算しておくこと。パラ
　　　　　　　　　　　　　メーターa と，計算する複素数平面の四角形の入力はあるよ。カラーは自分でときどき変えて見て下さい。
　　19)　 zroot.BAS ........ 複素数z を与えて，√z を計算・表示する。
　　20)　 Q2jb.BAS ........ プログラムをrunする前に，2種類の色系統を選んでおいて下さい。REMを取ったり，付けたりして， 2種類を決め
　　　　　　　　　　　　　る。また，吸引的周期軌道（固定点含む）は，プログラム Q2iteration.BAS で計算（反復回数tm=2000以上を使う）
　　　　　　　　　　　　　して，周期点を全てプログラムに書き込んでおいて下さい（書くのは大変だから，コピーコマンドを上手に使って!）。
　　　　　　　　　　　　　周期15以上には対応していないので注意（プログラム内のカラーを増やせば使える。読者がプログラム修正して！）。
　　21)　 Q2inv.BAS ........ q を反撥的固定点（or 周期点）として，方程式 Q(z)=q を解いて q の逆像を2つ計算。さらに，その2つの 逆像を
　　　　　　　　　　　　　計算する（全部で4つ）。これを16回くりかえし，得られた点を全てプロットする。点の数は，1つの q に対して
　　　　　　　　　　　　　　　　　　　　　2+4+8+ … +216=131070 （個）
　　　　　　　　　　　　　であるが，この3倍までの点がプロットできる。
　 このページのトップに戻る 　第1ルームの目次に戻る
♥♥♥♥♥♥♥♥♥♥♥♥♥♥ ♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥ ♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥ ♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥ ♥♥　　

　Study-r. 中学生，高校生のための数学勉強部屋； Vuestro estudio

（7月1日 '2020 アップデイト）
１．中学生のために
　　　　1-1．令和2年神奈川県公立高校入試問題（数学）の略解と解説。
　（令和2年4月20日，記）
　　　　新型コロナ騒動で家にいることが多く、時間が十分あるので、今年の神奈川県公立高校の入試問題（数学）の略解を作ってみようと思いました。
　　論文作成用のTeXを使って、約1週間くらいかかりましたかね。出来上がったので、PDFファイルとして読者がダウンロードできるようにしました。
　　これを利用する方は、問題自体は書いてないので、あらかじめ数学の問題を神奈川県公立高等学校のホームページから取得しておいて下さい。
　　　　改めて問題を解いてみて、問題の程度の高さに感心しました。大(だい)のおとなでも時間内(50分)に解くのは無理ですね。私の独断で各問に
　　レベルを付けました。

　　　　　レベル４　……　簡単な問題で、誰でもできるようなもの。
　　　　　レベル３　……　ごく普通の問題、教科書の例題や問題で難易度が中程度のもの。まあ、できてもらいたい問題。
　　　　　レベル２　……　教科書の例題や問題で，一番難しいと思われるもの。想像力と計算力が必要。ここまでできれば合格間違いないでしょう。
　　　　　レベル１　……　大変難しい問題、できなくてもしょうがないかな。このような問題は避けて、やり過ごす眼力も必要ですね。
　　レベル４とレベル３の問題がほぼできれば50点位はとれます。レベル３より上の問題がどのくらいできるかが合格の目安になるでしょう。

　　　　私の感想では、問題は多すぎます。レベル１、レベル２の問題も少し減らしたほうが良い。入学試験というものは、高校の授業内容について
　　いける様な、基礎学力があるかないかを見れば良いと考えます（大学入試も同様です；やたら難しくする必要はない）。
　　令和2年神奈川県公立高校入学試験(数学)の略解・解説 　　　　　1-2．令和3年神奈川県公立高校入試問題（数学）の略解と解説。
　（令和3年3月31日，記）
　　　　問題の略解と解説を書いてみました。今年の問題は，去年よりややいい問題で，少しやさしくなっていますかね。読者の皆さんはどう思い
　　ますか。入試問題と言っても，教科書で習った範囲の問題なので，落ち着いて考えれば解けますよ。教科書の問題がほとんど解ければ，入試も
　　合格点が取れると思います。数学の問題の解き方はたくさんあります。私の解答はそのうちの1つです。あなた独自の解答ができれば，それは
　　素晴らしいことです。私の解答を見ないで一度解いてみて下さい。
　　　　問題は，神奈川県公立高等学校のホームページから取得してください。私の解説は，pdf.ファイルになっていますので，ダウンロードして
　　カラー印刷して使って下さい。
　　令和3年神奈川県公立高校入学試験(数学)の略解・解説 　　　　1-3．テキスト１；絵とともに学ぶ中学数学「数・式の計算・関数・方程式」
　　　　　　　　　　第1章　数と演算について　　　第2章　関数とグラフ　　　第3章　方程式とその解
　　テキスト１；絵とともに学ぶ中学数学「数・式の計算・関数・方程式」 　　　　1-4．テキスト２；絵とともに学ぶ中学数学「平面図形とその応用」
　　　　　　　　　　第1章　多角形　　　　　第2章　円
　　テキスト２；絵とともに学ぶ中学数学「平面図形とその応用」 　　　　1-5．テキスト３；絵とともに学ぶ中学数学「空間図形，確率・統計」
　　　　　　　　　　第1章　空間図形　　　　　第2章　確率・統計
　　テキスト３；絵とともに学ぶ中学数学「空間図形，確率・統計」 　　　上のテキスト(参考書）は誰もが使えます。ダウンロードして，カラーで印刷してください。あなたの役に立てばとてもうれしいですね。絵を沢山
　　とりいれ，わかりやすいテキストを目指しましたが，いかがでしょう。間違いやまずい所があったら教えて下さい。順次訂正し，よいテキストにして
　　いきます。
　　　これらのテキストは，入試のための総復習として利用するのがいいですかね。中3の夏休みや冬休みに集中して 勉強してくれれば有効だと思うよ。
　　３つのテキストは，これからさらにアップデートしますので，どんどん使いやすくなると思います。乞うご期待！
　　テキスト１は，章末問題を追加して，問題演習を充実させました。問題に挑戦してよ。（8月20日 '21，記）

　　　　　1-6．令和4年神奈川県公立高校入試問題（数学）の略解と解説。
　（令和4年4月9日，記）
　　　今年の入試は難しかったね。また，2年来のコロナ禍で，受験生は精神的に落ち着かなかったと思います。3月に入ると，ウクライナで戦争が
　　始まり，不安な社会に追い打ちをかけているようで，怖いですね。しかし，こんな時代にこつこつ数学の勉強をするのもいつか役に立つでしょう。
　　決して無駄にはなりませんよ。頑張りましょう。
　　　数学の問題は，あらかじめ神奈川県公立高等学校のホームページから取得しておいて下さい。問題は1時間位かけて自分で解いて見てね。そして，
　　私の解答と比較してみて下さい。数学の問題は，いろいろな解法があるので，自分流のやり方で解いていいのです。私の解法にこだわることはあり
　　ません。答えに行き着けばいいのです。私の解説は，pdf.ファイルになっていますので，ダウンロードしてカラー印刷して使って下さい。
　　令和4年神奈川県公立高校入学試験(数学)の略解・解説 　　　　　1-7．令和4年東京都公立高校入試問題（数学）の略解と解説。
　（令和4年6月16日，記）
　　　東京都の問題は初めて解説します。問題冊子は東京都のホームページから取得しておいてください。問題冊子はなくても，私の解説文は読めます
　　が，図や表の表示が原文とちょっと違いますので，注意して下さい。
　　　問題を解いて見た感想は，「ちょっと易しすぎるかな」です。問題が易しいのは歓迎しますが，ちょっと骨のある問題がほとんどありませんでし
　　た。やたらに難しい問題は２つありましたね。問題全体としては，難易度のバランスが取れていなかったようです。これが私の評価ですが，読者の
　　皆さんは，自分で解いて見て，私の解答と比較して見て下さい。じっくり解答することで，確実に数学の力が付きますよ。Let's try!!
　　令和4年東京都公立高校入学試験(数学)の略解・解説 　　　　　1-8．令和5年神奈川県公立高校入試問題（数学）の略解と解説。
　（令和5年4月2日，記）
　　　数学の問題は神奈川県公立高等学校のホームページから取得しておいて下さい。コロナ禍が収まりそうになっていますが，数学の勉強はいかが
　　ですか。問題は50分で解いてみて（多分50分ではできないので，できるまでやるのがいいかな），そして私の解答と比較してみて下さい。今年の
　　問題は，去年よりかなり難しかったよ。問題文もけっこう長くなっているので，しっかり読んで，内容を正確に把握することが大切ですね。長い
　　文章の応用問題などは，普段の練習がものをいいますよ。私の解説は，pdf.ファイルになっていますので，ダウンロードしてカラー印刷して使って
　　下さい。
　　令和5年神奈川県公立高校入学試験(数学)の略解・解説 　　　　　1-9．令和5年東京都立高校入試問題（数学）の略解と解説。
　（令和5年4月23日，記）
　　　問題は，東京都のホームページから取得しておいてください。私の解説文は，図は原文と少し違っている（コピーではなく私が自分で描いた）と思い
　　ますので，注意して下さい。問題を解いてみた感想は，”超・難しい問題が３つもあった”ということです。他の問題はまあまあ易しかったので，多く
　　の受験生は，70点位は取れたのではないかと思います。去年と同様に，問題全体としては難易度のバランスが取れていなかったようです。読者の皆さん
　　も，50分で解いてみて，私の解答と比較して下さい。解説文は，pdf.ファイルになっていますので，ダウンロードしてカラー印刷して使って下さい。
　　令和5年東京都立高校入学試験(数学)の略解・解説 　　1-O．中・高生のための数学読本：数とはなんぞや --数は誰がつくったの，どこにあるの--
　　　　　第１章．いろいろな数　§1.1 自然数，ゼロ，整数，数直線　§1.2 有理数，有限小数，循環小数　§1.3 三平方の定理，無理数，実数
　　　　　第２章．整数の性質，方程式の解　§2.1 素数，整数の性質　§2.2 数学の命題について　§2.3 素数の性質　§2.4 方程式の解
　　　数(すう)に，強い人も弱い人も一度読んでみて下さい。数は誰が作ったのか，どこにあるのか，どんな性質をもっているのか，どんな役に立つのか，
　　すっきりわかるかもね？　わかんなかったらもう一度読んでみてね。カラーの図や絵がいっぱいあるので，見てるだけでも楽しめるかもね。
　　　このテキストは，pdfファイルでできています。ダウンロードしてカラー印刷のうえ，使ってみて下さい。 Let's play with numbers!
　　　 　　中・高生のための数学読本：数とはなんぞや--数は誰がつくったの，どこにあるの-- 　　1-P．　小論：中・高・大学生のための「パイソンでグラフを描こう」
　　　　0)　パイソン(Python)について　　1)　1次関数と2次関数　　2)　三角関数，指数関数など　　3)　逆三角関数，二変数関数など
　　　プログラム言語パイソンは，すごく使いやすいよ。数値データを集合として扱っているところが，新しい言語らしいかな。 平面上のグラフ
　　は簡単に描けます。さらに，二変数関数の曲面表示はその難しさを意識することなく， 誰にでも扱えるところが優れているね。
　　チャレンジしてよ！
　　中・高・大学生のための「パイソンでグラフを描こう」 ２．高校生のために
　　2-1．令和2年大学入試センター試験（数学U・数学B）の略解と解説。
　（令和2年5月6日記）
　　　　試験問題は，読者の皆さんが各自手に入れて下さい。とにかくゆっくり解いてみました。第1の感想は，“これは数学の問題じゃないな”，
　　ということです。考えて解答の道筋を見つけるということ（これが問題を解くということなのだが）は必要なく，“問題文の言うがままに，計算
　　などをやって，穴を埋める作業を続ける”というのが，センター試験です。一言で片づけると“面白くない”ね。そして，問題文が“美しくない”。
　　こういう問題を塾などで一生懸命やっている高校生は，数学嫌いになっても不思議じゃないね。数学者の端くれとしてこういう試験は嫌いだね。
　　　　今後の共通テストでは，学生に考えさせる問題，全体をまとめる能力を見るための，記述式問題の導入を考えている様だが，採点は大変難しく，
　　また採点者によって不公平が生じるので，これも止めてほしいね。全国一斉のテストでこの様な知識を要求するのは無理ですよ。私の考えでは，
　　共通テストは，大学の授業内容についてこれる様な基礎学力があるかないかを見る試験， と位置付けてほしい。それで十分でしょう。もっと特殊
　　な能力をみたいのなら，各大学で（2次試験として）独自の試験をやればいいのです。だから，共通テストは今のセンター試験より難しくする必要は
　　ないよ。もうちょっと易しくてもいいね。そして，もうちょっと考えるような問題を増やし，答えも5択問題とか10択問題も入れるといいね。試験
　　時間は70分にしてよ。共通テストを利用する大学は，共通テストだけで合否の判定をしてもいいし，足切りに使って2次試験では，本当の数学らしい
　　問題を出す，ということにすればいいんじゃない。
　　　　私の略解と解説では，各問題にレベルを付けました。レベルづけの基準は中学生の所で示したやり方と同じです。レベル４とレベル３ができれば
　　55点位になります。競争率の高い大学だとレベル２の問題も半分くらい解けないと合格は無理かな。
　　令和2年大学入試センター試験（数学U・数学B）の略解・解説 　　2-2．令和3年大学入試共通テスト（数学U・数学B）の略解と解説。
　（令和3年2月2日記）
　　　　試験問題は，各自入手して下さい。今年は共通テスト元年でした。まあまあ，あまり難しくないいい問題ができてますね。いつも思うのだが，
　　この問題を60分で解くのは大変ですね。難しい問題は避けて行くという能力も必要ですな。私は，問題の偏りが少し気になったね。問題の解き方や
　　計算法などは，いくらでもあるので，私の解答は単なる参考にしてよ。とにかく，ゆっくり自分で解いて見て私の解答と比較してみて下さい。
　　ダウンロードしたファイルは，カラー印刷してお使い下さい。4色ほど使ったファイルです。
　　令和3年大学入試共通テスト（数学U・数学B）の略解・解説 　　2-3．漸化式を含む差分方程式の解について
　　　　数列とともに学ぶ漸化式は，苦手な方が多いかもしれませんが，漸化式を含む差分方程式を統一的に学べば，その理論は単純です。漸化式の
　　解の世界がどんなものか一目瞭然となります。この小論は高校生の知識で十分理解できます。さあ，読んでみて下さい。
　　漸化式を含む差分方程式の解について 　　2-4．令和4年大学入試共通テスト（数学T・数学A）の略解と解説。
　（令和4年3月18日記）
　　　　試験問題は，各自入手して下さい。この試験は，過去最低の平均点37.96で話題になりました。何が難しかったのでしょう。解いてみた感想は
　　本当に難しい問題がいくつかあったということです。数学者の出す問題は，得てして難しくなりがちです。受験生の力がよく分かっていないという
　　こともあるでしょう。学生さんは問題を解いてみて，私の解答（解答は1つではなく，いろんな解き方があるので，私の解法に固執しないで下
　　さい）と比較して下さい。問題は，けっこういい問題なので楽しめますよ。ダウンロードしたファイルは，カラー印刷してお使い下さい。
　　令和4年大学入試共通テスト（数学T・数学A）の略解・解説 　　2-5．令和4年大学入試共通テスト（数学U・数学B）の略解と解説。
　（令和4年5月14日記）
　　　　試験問題は，各自入手して下さい。コロナ禍で受験生は大変でしたよね。授業をまともに受けられなかった方々も沢山いたことと思います。
　　今年の平均点は，昨年より16点も低かったですね。問題は，本当に難しかったでしょうか？ 私の見る限り，すごく難しかったという問題ではない
　　ですね。内容のバランスも良く，まあまあいい問題がそろっていましたよ。しかし，問題文がけっこう長くなっていますね。読解力と忍耐が必要な
　　問題になっています。これに耐えられるか否か試されている様です。
　　　　前々から思っていますが，試験時間が60分と言うのは，じっくり物事を考える学生にとっては，短いですね。できれば70分位にして欲しいね。
　　関係者の方々の再検討を望みます。
　　令和4年大学入試共通テスト（数学U・数学B）の略解・解説 　　2-6．令和5年大学入試共通テスト（数学U・数学B）の略解と解説。
　（令和5年2月17日記）
　　　　試験問題は，各自入手して下さい。コロナ禍が長引き，ロシアのウクライナ侵略戦争も解決の道筋が見えない世界情勢です。受験生も落ち着いて
　　勉強できないよね。今年の問題は，去年の反動か？　けっこう易しかったね。平均点は　61.48でしたが，平均点以上取れましたか？　去年と同様に
　　問題文がけっこう長くなっていますね。読解力と忍耐が必要です。このような問題に慣れましたか？　しかし，解答の道筋を与えてくれているので，
　　難しくはないですね。解けなかった問題があったらもう一度やってみてください。そして，私の解答と比較してよ。数学の解答は，一通りではなく
　　いっぱいありますよ。自分の好きなやりかたで解答を見つけて下さい。ダウンロードしたファイルは，カラー印刷してお使い下さい。
　　令和5年大学入試共通テスト（数学U・数学B）の略解・解説 　　2-7．令和5年大学入試共通テスト（数学I・数学A）の略解と解説。
　（令和5年3月13日記）
　　　　試験問題は，各自入手して下さい。今年の問題もけっこう難しかったね。しかし，易しい問題も多かったので，平均点はそんなに悪くなかった
　　ですね。受験生にじっくり考えさせて，計算なり結論なりをまとめさせようという問題を出しているようなので，問題文と説明文がやたら長くなって
　　いますね。すばやく読んで問題の要点を把握しなければならないので，国語力も必要ですね。
　　　また，不定方程式は2年連続出ていますよ。この解法はけっこう難しいので，しっかり練習しておいたほうがいいですね。
　　　読者諸君は，自分で問題を解いて見て，私の解答と比較してみてください。数学の問題では，解答の方法はいくらでもありますから，自分の好きな
　　解法でやってみてください。やってみることで，数学の力はアップしますよ。ダウンロードしたファイルは，カラー印刷してお使い下さい。
　　令和5年大学入試共通テスト（数学I・数学A）の略解・解説
　　2-8．令和6年大学入試共通テスト（数学I・数学A）の略解と解説。
　（令和6年3月16日記）
　　　　試験問題は，各自入手して下さい。今年の問題は難しくはなかったけど，慣れていないn進数などの問題が出て戸惑ったでしょう。また，一昨年
　　も出ていた，メネラウスの定理を使う問題もありました。メネラウスの定理しっかり使えましたか？　整数解を求める不定方程式は3年連続出ました
　　ね。不定方程式はもう，必ず出ると思って練習した方がいいですね。しかし，今年のはやたら難しかったね。
　　　　問題文と説明文がやたら長くなっているので，問題の要点をすばやく把握する訓練が必要ですね。国語力も身につけて下さい。
　　　　また，数学の問題では，解答の方法はいくらでもありますから，自分の好きなやりかたで解いてみて下さい。入試問題を自力でやってみること
　　で，数学の力は確実にアップしますよ。じっくり考えると”楽しい”と思える問題もあるよ。
　　　　ダウンロードしたファイルは，カラー印刷してお使い下さい。
　　令和6年大学入試共通テスト（数学I・数学A）の略解・解説 　　2-9．令和6年大学入試共通テスト（数U・数学B）の略解と解説。
　（令和6年4月5日記）
　　　　試験問題は，各自入手して下さい。今年の問題も昨年に続き比較的易しかったね。あなたの出来はいかがでしたか。超難問もなかったですね。
　　しかしながら，教科書や参考書などではほとんど扱わない問題（私は特異な問題と呼ぶ）が出てましたよね。出題者の説明も長々とあったんですが
　　ついていけましたかね。最近は，問題文が長く，読解力と忍耐が必要なものが多くなりましたね。普段から，応用的な問題を解く訓練しておいた
　　ほうがいいですね。
　　　　これから受験する読者は，問題を最後まで自分で解いてみて（私の解答は見ないこと，わかるまで自分で考えること。時間はなんぼかかっても
　　よい），最後に私の解答と比較してみて下さい。じっくり学ぶことで，力つきますよ。
　　　　ダウンロードしたファイルは，カラー印刷してお使い下さい。
　　　　 　　令和6年大学入試共通テスト（数学U・数学B）の略解・解説
3．番外編
　　3-1．「令和3年　開成中学校入試問題（算数）」考　−略解と解説を踏まえて−
　　　　令和3年2月6日(土）の朝日新聞に，開成中学の入試問題（算数）がのっていました。ちょっと興味があったので解いてみましたが，大変難し
　　かったですね。中学入試に興味のある方々は，略解と解説を書いたこの論説をじっくり読んでみて下さい。特に，私立中学を目指す小学生の方々
　　およびご父兄の皆さんは，一度問題をやってみることをお勧めします。やってみた感想を教えていただければ嬉しいですね。
　　　　問題文は，開成中学のホームページから入手して下さい。この論説は，pdfファイルになっていますので，ダウンロードし，カラーで印刷して
　　お使い下さい。
　　「令和3年　開成中学校入試問題（算数）」考　−略解と解説を踏まえて− このページのトップに戻る 　第1ルームの目次に戻る
♥♥♥♥♥♥♥♥♥♥♥♥♥♥ ♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥ ♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥ ♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥ ♥♥　　

♠øøøøøøøøøøøø♣ℵℵℵ ℵℵℵℵℵℵℵ♥ββββββββββ ♦ξξξξξξξξξξ♠∇∇∇∇∇∇∇∇∇∇ ♣ℜℜℜℜℜℜℜℜℜℜ♥ΘΘΘΘΘΘΘ ΘΘΘΘΘΘ♦

　J-o. おとといのジョーの独り言； Mis monólogos

　　　ここは，私の独り言の部屋です。ふだん考えていることを書きなぐってみました。こんな奴もいるんだなあ，と，まあ読んでみて下さい。
　　しかし，少しは気にして考えて下さい。考える人が増えれば，日本はきっと面白くてよい国に変わるでしょう。

　１．日本のプロ野球をもっと面白くして。　私は国鉄スワローズ時代からのヤクルトファンです。 王，長島，金田は我らのスーパーヒーロー
　　でしたね。プロ野球は巨人を中心に回っていて，マスコミなどもこの状況に追随していましたね。パリーグはおまけみたいな存在でした。
　　そんな，古きよき時代からの野球ファンです。弱いチームを常に応援していたので，ひいきのチームは国鉄スワローズだった。その後も，
　　ずーっとヤクルト（サンケイの時代もあったね）ファンで，広岡監督のもとで初優勝した時は感激したね。”やっと私の時代が来た”という
　　感じでした。
　　　　野茂さんが単身大リーグに乗り込んだときも興奮したね。ラジオで大リーグの実況中継を聞いたりしたこともあったよ。BS放送での大
　　リーグ中継が始まってからは，良く見るようになった。イチローの大活躍でMLBは身近な存在になったし，去年からは大谷ブームに引きず
　　られて，アメリカのファンと同様にMLBの試合を楽しんでいるよ。そして，私にとって，日本のプロ野球の魅力はどんどん薄れてきました。
　　　　日本のプロ野球がつまらなくなった極め付きの理由は，クライマックスシリーズなどという下らないことを始めたからです。ペナント
　　レースで勝ったチームが1番強いのは，誰が考えても当たり前のことなのです。従って，リーグ優勝した2チームで日本一を争うのが当然な
　　のです。日本野球機構は，この単純な理屈を尊重すべきだね。私のような野球ファンにとっては，クライマックスシリーズの押し付けは日本
　　野球機構のパワハラ以外の何物でもありません。去年の日本シリーズの覇者ソフトバンクの工藤監督は，優勝を心から喜んではいなかった
　　ように見えた，のは私だけでしょうか？ 兎に角，クライマックスシリーズはやめましょう。あなたはどう思いますか？ 野村さん（元ヤク
　　ルト監督）はどう思いますか？

　　　　MLBは，いろんな国から個性ある優秀な選手が集まって来て，競い合っているので面白いのです。日本の選手もMLBで十分やれるという
　　ことも分って来ました。日本の隣国に目をやったとき，韓国，台湾には素晴らしい選手がいますよね。中国にもいるかもしれませんね。21世
　　紀に入り，世界がすごく狭くなっている現在，日本のチームだけのプロ野球リーグという考えは捨てた方がいいですね。
　　　　韓国，台湾，中国および日本の球団で東アジアリーグを作ることを提案します。このリーグは，メジャーリーグ18チーム，マイナーリー
　　グ15チーム位でスタートします。メジャーリーグは6チームずつでグループを作り，それぞれ，“ウエスタン”，“セントラル”，”パシフィグ
　　リーグ（仮の名称）と呼びましょう。チャンピオンシップは，各リーグの優勝チームとリーグ2位の最高勝率チームの4チームでトーナメン
　　ト形式で戦います。3つのリーグの交流戦は当然やります。1チームの試合数は，リーグ内の試合が110（各チームと22試合），交流戦が36
　　（各チームと3試合）の合計146試合でいかがですか。シーズンの最後には，マイナーリーグの上位3チームとメジャーリーグの最下位3チー
　　ムとの入れ替え戦をやります。また，優秀な選手はどんどんアメリカの大リーグに挑戦できるようなシステムにしましょう。
　　　　1年目はどうしますか，メジャーの18チーム（18にはこだわらない，15でもよい）をどうやって選びますか？ という質問はおありでし
　　ょうが，これらのことをどうやって決めるかは日本野球機構の仕事でしょうね。私も意見はありますが，まあ，皆でよい方法を考えましょう。
このページのトップに戻る

　２． 原発はやめようよ。 福島第１原発の汚染水タンクはどんどんドンドン増えていきますね， 原発周囲の地中に氷壁を作りましたが，基本的
　　に汚染された地下水は海にたれ流しです。汚染水タンクもいずれ腐って穴があき，水が漏れるでしょう。汚染土壌を集めた袋も捨て場が無く
　　置きっぱなしですね。いずれ，原発周辺は汚染水タンクでいっぱいになり，そうこうするうちに，福島県全体が汚染物質だらけになるよね。
　　きちんとした対策が取られていないので，私はこのように考えています。あなたは，どう思いますか？
　　　　メルトダウンして融けた燃料棒デプリをどうやって処理するのですかね，何年で処理できるのですか（100年？），費用はいくらになり
　　ますか（一基1兆円？），そしてどこへ捨てますか（300m以深の地下で岩盤が強固な所，日本のどこ？），政府は何も決めていませんね（決
　　められませんね）。既に，皆が分っているように，原発に一度重大な事故が起こったとき，人間はもう制御できません。人の手に負える代物
　　ではないことが明白です。津波で破壊された福島第一原発の水素爆発（2011年3月12日），チェリノブイル原発の爆発事故（1986年4月26
　　日）がこのことを証明しています。チェリノブイル事故からは33年経過しましたが，放射能が原因で死亡した人は数万人と言われています。
　　廃炉作業もまだ終わっていません。今も30キロ圏内は立ち入り禁止です。人類は核エネルギーの利用から手を引くべきです。

　 　　　小泉元首相は，スウェーデンの原発施設の視察から帰った後，“原発即廃止” を訴えています。高濃度放射性廃棄物の捨て場所を確保す
　　ることの困難さを言っています。首相のときは深く考えなかったが，“視察をしてよく理解した”，また，“過ちては改むるに憚ること勿れ”
　　とも言っています。私は，これは正しい判断だと思います。しかし，自民党の政治家は何もしませんね ．．．??　情け無いね。
　　　　ドイツのメルケル首相は福島の惨事をを見て，“ハイテク大国日本ですら，原発を安全に運転できない” と述べ，2022年までに全原発を
　　停止することを，国として決定しました。そしてすぐ，再生可能エネルギーの利用に方向転換しました。再生可能エネルギーの生産は難しい
　　ことが沢山あるようですが，ドイツは頑張っています。日本は，１歩も２歩（いや，数歩）も後れを取っています。残念ですね。
　　　　経団連会長の中西さんは，政府の原発継続方針に関して，“エモーショナルな反対をする人達と議論をしても意味がない。絶対いやだと言
　　う方を説得する力はない”（3月11日 '19）と述べています。反対する方々を感情的と決めつけるのはいかがですかね。人間は核エネルギーを
　　制御できないことを我々は見てきたんです。エモーショナルではありませんよ。中西さんは原発反対派と議論したいのですか，そして考えを
　　変えさせたいのですか？　たぶんそれは無理ですよ。なぜなら，しつこいけど，我々は失敗を2度も見たのだから。互いの意見を分りあうこと
　　はできても，変えさせることは不可能だよね。
　　　　どうあれ，“原発即廃止”を決定し，今すぐ再生可能エネルギーの量産に全力を傾けてほしいね。電力が足りないなら，いつでも使用規制
　　（節電）に協力しますよ。東日本大震災の年は，国民の多くが節電に協力したよ（政府のお偉方さん，もう覚えていないのかい？）。今は，
　　電気の無駄遣いもすごく気になるよ。
このページのトップに戻る

　３．日本が世界をリードしようよ！　坂本龍馬は，約１世紀半も前に，“日本は力をつけて 列強（アメリカ，フランス，イギリス，ロシアなど）
　　から独立して独自の道を歩かなければならない”と言ったと聞いています。残念ながら，この理想は未だに実現されていません。世界の人々は，
　　2回も悲惨な世界大戦を経験したにもかかわらず，まだ懲りずに戦いを続けています（アフリカや中東など）。戦争は勝っても負けても本当に
　　残酷なものです。日本人は，肉親や親戚・友人などの戦死を通じて多くの体験をしてきたので，このことが良く分っています。もし，今度大
　　きな戦争が起これば，どこかの国が原爆を使うかもしれません。その時は，人類が滅亡するか地球が破壊されるかのどちらかでしょう。もう，
　　血を流し，国々を爆破するのは止めましょう！
　　　　世界は，未だに力の論理（いわば，やくざの縄張り争い）で動いています。即ち，武力の強い所が威張っている構図です。大昔とちっと
　　も変ってないよね。“人間は理性をもった動物である” と習って来ましたが，理性はどこへ行ったの？　日本はアメリカべったりで，独立国と
　　は言えませんね。アメリカの核の傘のもとにいるから，核兵器禁止条約にも賛成していません。情け無いね，広島，長崎は何だったの？

　　　　日本が世界をリードしていくための，おとといのジョーの考えを述べます。まずアメリカから独立することです。日米安保条約は解消し，
　　新たな友好条約（対等な二国としての）を結びます。当然，米軍基地は全て引き払ってもらいます。これで沖縄の問題はほとんど解決します。
　　次に，永世中立国を宣言します（これは国連で認めてもらいましょう）。欧州におけるスイス，オーストリアがよい見本です。自衛隊は存続
　　させましょう。永世中立国といっても，外国からの一方的な攻撃に対しては，この国を守らなければなりません。今，実施している自衛隊の
　　海外派遣はやめます。戦争を放棄した日本国憲法は変える必要はありません。日本国憲法の精神は，日本が永世中立国になることでかえって
　　輝きを増すでしょう。永世中立国をめざすこのような考えは，欧州統合が実現している今日，夢物語ではありません。現実的なものですよ。
　　さあ，皆さん実現させましょう！
　　　　永世中立国となった日本は，フランス革命のスローガンであった，自由（Liberté）・平等（Egalité）・博愛（Fraternité）および戦争放
　　棄の日本国憲法の精神のもとに世界の国々と対話し，外交活動を展開します。倫理・哲学にのっとった良識的判断を世界に示していくことで，
　　アメリカやロシア・中国とは異なった日本独自の見解が出てきます。そうなったとき，多くの国々が日本の考えを支持し，日本を手本にする
　　でしょう。
　　　　国連は，戦争一つ止められないですね（例えば，シリアにおける戦争）。どうしてですか？　常任理事国の拒否権がじゃまをしてますね。
　　常任理事国は未だに力の論理・利権政治で動いているからです。こういう体質を，日本は変えていかなければなりません。国連は世界の平和
　　のためにあるのですよね，その役割を果たしましょうよ。

　　　　さて，現実の国会（政治）は，自・公連立政権の多数者の専制によって動いていますね。野党との話し合いは十分でなく，国民にも説明
　　不足で納得のいかない形でずるずると進行してます（少なくとも私は，納得していない）。日本は“民主主義の国”と言われていますが，私が
　　政策について発言する機会も，地元の政治家が有権者に説明したり，有権者の意見を聞いたりするということも全くありませんよ（共産党の
　　み，たまに意見を聞くことがある，えらい！）。さあ，民主主義とは一体なんでしょうか？　みずから，政治の世界に入って行かなければな
　　らないのかな・・・。もし，国政選挙に立候補したいと思っても，衆・参の選挙区では300万円，比例区では600万円の供託金を出さなけれ
　　ばならないよ。普通の人はここでめげるよね（もちろん，得票数がある値を超えれば供託金は戻ってきますが．．．）。政治って特異な世界
　　だなあ・・・と感じて，興味無くなるよね。アメリカやフランスでは供託金はないよ，立候補したい人は誰でも立候補できます。日本だけが，
　　すごく高い供託金を払わなければならないのです（馬っ鹿みたい 😡）。
　　　　政治は，時々政権が交代しないとよくなりませんよね。しかし，今の日本は交代すべき野党が信頼されていないし，政権を取ろうと思って
　　ないように見えます。自分の小選挙区で，強い与党の人が1人と，野党から2,3人の立候補者が出たとき，与党嫌いの有権者は誰に投票します？
　　投票する方は白けちゃうのです（このような人達は棄権するでしょう）。野党は，合併しなくてもいいのです。立候補者を一人に絞って下さ
　　い。そして政策で勝負するのです。こんな方法が，政権交代に近づく第一歩です。国民のために，今より少しでもよい政治を目指し，団結し
　　てよ。このような切磋琢磨で，政権交代が時々あれば，日本の政治はすごくよくなるよ。
　　　　政治家はもちろんのこと，有権者も，もっともっと日本のことを考えなくちゃだめだよ。医療費，教育費，交通費は今の5分の1位（ただ
　　が一番だが．．）にしようよ。自分の国なんだから堂々と主張しましょう。この3つの分野にお金を集中させましょう。有権者は自分の頭で考
　　えて，悪いことは悪いと主張し，よいことはあらゆる機会をとらえて要望しましょう。政権がよくないと思ったら，交代させましょう。これは，
　　我々国民の意思で（選挙で）できるのですよ。

　　　　現政権のもとでは沖縄の問題は解決しません。「沖縄の米軍基地のほとんどを，本土に移しましょう。例えば，人口密度の低い，北海道，
　　岩手県，秋田県へ」という政策は実行できますか？　この地域の住民の皆さん賛成していただけますか？　これができなければ，まあ，無理
　　ということです。私が最初に言ったように，日米安保を解消すれば，自然に解決します。
　　　　私の考えでは，沖縄は日本から独立した方がいいと思います。もともと琉球国として独立した国家なのだから，日本からの独立を宣言した
　　らいかがですか？　少なくとも私は賛成します。現状のままでは，この策が最善でしょう。本土の皆さんも考えて下さい。
　　　　今の日本の政治（社会）は，付和雷同・忖度（長いものには巻かれろ）政治（社会）になっていませんか。これは本当に本当によくないよ。
　　一人一人が精神的に自立し，自分の考えで物事を決定すべきです（吉田松陰も福沢諭吉もこのことをいつも言っていたように思います）。
　　　　　　　　　　　　　　　　　　　　　The most important thing is to believe in yourself.
このページのトップに戻る

　４．横浜市のIRカジノ構想に反対、市長は市民を馬鹿にしていませんか？
　　(3月26日 '20　記）
　　　　IRカジノ構想に対する推進案（「IR総合型リゾートの推進」4億円）が、昨日（3月25日(水）,2020年）の会議で通過したというニュースを
　　見ました。横浜市では、今、市民からのパブリックコメントを3月6日から4月6日まで受け付けると言ってますよね。これを無視して、どうして
　　法案が通ってしまうの？　市民の意見は全く聞かないのかい？　市長は、我々市民を馬鹿にしているとしか思えないね（何のためのパブリックコ
　　メントですか）。政治っていったい何なの……　政治って、国民が主人公だよね、このことを忘れていませんか？
　　　横浜市民の私は、3月24日(火）'20 に次のようなパブリックコメントをメールで市に送りました。市民は誰でも送ることができるよ。メール
　　アドレスは、 yokohamair_ikenbosyuu@sic-kk.co.jp だよ。しかしながら、議員の誰がパブリックコメントを真剣に 読んでくれるのでしょうか、
　　期待できませんね。．．．

−−−−−−−−−−−−−−−−−（ここからパブリックコメント内容）−−−−−−−−−−
　　　IRカジノ構想に対する反対意見

　　　その1)　横浜市の未来（近い将来も含む）に対して建設的でない（希望が持てない）。

　　　　　　市政の大きな目標は、将来を担う子供たちを立派に育てることです。同様に、市
　　　　　民の意見・望みに耳を傾け、市民のための政治を実行することです。横浜市のIRカ
　　　　　ジノ構想は、より良い未来を創るという観点から、まったくはずれた所にあります。
　　　　　その必要性が全然分からない。
　　　　　　今も将来も、必要なものは子供達が自由に遊べる空間です。自然がいっぱいあ
　 　　　　る空間です。大都会（東京、横浜など）の住宅密集地には、子供が自由に遊べる空
　 　　　　間は全くと言っていいほどありません。子供は子供の頃徹底的に遊ばないと、成長
　 　　　　にゆがみが生じます。多くの遊びから健全な青年が育くまれます。そんな空間を横
　 　　　　浜市に作っていただきたい。例えば、

　　　 　　　 a)　自由に走り回れるのっぱらがあること
　　　　　　　b)　釣り場（海釣り、淡水釣り）があること
　　　　　　　c)　サッカー場、野球場、テニスコートがあること…（注1）
　　　　　　　　これらは、基本的に使用者が管理・運営
　　　　　　　d)　ニューヨークのセントラルパークのような、自然豊かな公園があること
　　　　　　　　ここでは、トンボ、蝶、種々の昆虫の観察が可能なこと。蛍が生息できれば完璧。
　　　　　誰もが、一日ここで遊べるそんな空間を創っていただきたい。

　　　 　　その2)　誰がカジノにいきますか。

　　　　　　私の友人で、カジノに行きたいという者は一人もいません。市役所にお勤めのあ
　　　　　なたの友人で、カジノに行きたいという方は何人いますか。聞きたいものです。私
　　　　　の想像では、カジノに行きたいと思う市民は１％位だと思います。横浜のカジノを
　　　　　目指して来日する観光客は、何人になるかは分かりませんが、それほど多くはない
　　　　　でしょう。というのは、日本を目指す観光客の目的はカジノではないということが
　　　　　想像できるからです。
　　　　　　かつて、パチンコという娯楽がにぎわいました（40年〜50年位前）。当時は、一
　　　　　般市民が楽しめる娯楽でした。千円もあれば十分遊べたし、沢山玉がでれば、景品
　　　　　と取り換えることが出来ました。景品として、食料品や生活必需品がたくさん置い
　　　　　てありました（私はいつもカニの缶詰をとってたね）。ところが、いつの間にか
　 　　　　　パチンコ屋は、様変わりしてしまいました。2,3千円では、まったく玉が出なくなり
　　　　　ました。1万円も30分くらいでなくなってしまうようになり、パチンコから遠ざかり
　　　　　ました。今のパチンコ屋では、プロかセミプロの方々が多い様です。そして、借金
　　　　　で経済破綻していく方も多いと聞いています。一般の多くの市民は、パチンコ屋に
　　　　　は行かなくなっています。カジノもまたしかりでしょう。
　　　　　ほとんどの市民が望まないカジノはやめましょう。

　　　 　　　その3)　カジノで税収はいくらになりますか。

　　　　　　市では、増収は1200億円位だと言っています。この程度のお金で何ができますか？…（注２）
　　　　　市長は、増税分を何に使うかはっきり述べていません。横浜市の将来のためにお金
　　　　　をどう使うか、きちんと述べてください。
　　　　　私の望みは、次のことに税金を使って欲しいということです。

　　　 　　　a)　大学までの学費を負担すること（市民に対して）
　　　　　　 b)　70歳以上の市民の医療費と交通費の負担

　　 　　　　　1200億円程度の増収では、上の2つのことは実現できないことは明らかですよね。
　　　　　と言うことは、抜本的な市政の改革をやらないと、上の2つは実現できないよね。だか
　　　　　ら、政治家の皆さんに知恵を絞ってもらって、これらを実現するための方法を模索して
　　　　　もらいたいのです。私の述べていることは、絵空事ではありませんよ。世界では、この
　　　　　位のことをやっている市はありますよ。調べてみて下さい。
−−−−−（以上です）−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
　　　（注1）野球場、サッカー場は数個、テニスコートは20面位必要。
　　　（注2）現在、横浜市の人口は375万人くらい、15歳未満が45万6千人くらい、
　　　　　（1200億円）÷（45万6千）＝26万3千円。これでは、学費などは負担できないよ。
このページのトップに戻る

　５．プーチンさん戦争はやめましょう！
（3月25日　'22記）
　　　　プーチンさん（さん付けはしたくないが，一応ロシアの大統領なので，最初だけさんを付けます）あなたは間違っていますよ。やって
　　　ることは侵略と殺人です。自国の軍隊・軍人のやっていることを把握してませんね。史上最悪の侵略戦争です。Stop War immediately!
　　　　プーチンは，ウクライナにはネオ−ナチがはびこっていると叫んでいますが，プーチンとその側近こそがネオ−ナチだよね，あんたらは
　　　臆病で卑怯な政治家だよ（You are cowardly and dirty politicians)。善良な市民を何人殺せば気が済むんだい。
　
　　21世紀は，どこの国の誰でもが海外旅行できるし（できない国もいくらかあるようですが，改革を望む），国際的なさなざまなニュースを見聞き
　　することもできる時代です。例えば，プロのスポーツ選手は，世界を渡り歩き試合を楽しみながら，賞金も得ることができます。海外に多くの友人
　　がいる選手も多いことでしょう。こんな，開かれた21世紀において，ロシア（プーチンさん）は何をやっているのでしょう。少なくともアジアの
　　1員である私にはさっぱり分からないよ。ウクライナがどんな政治体制になろうとも，独立した国家なのだからプーチンさんが文句を言う理由は
　　ないよね。隣国として仲良くやっていけばいいんじゃありませんか(政治体制と国家間の貿易・経済活動などは切り離して考えればいいのです）。
　　　世界の多くの方々は，海外旅行などを通じて，いろんな国のいい所・悪い所を見聞することができます。そして，自分の国のいい所・悪い所を
　　判断できるようになります。政治や社会制度の改革も自分の頭で考えることができる時代になっています。平和で安全な良い国が少しずつ増えていく
　　のは歴史の必然です。これをストップさせる権利は誰にもないよ。
　　　いまは，ウクライナに何らかの支援をしましょう！ ウクライナへの支援金は，郵便局から公益財団法人日本ユニセフ協会に送るのが安全ですね。
　　通信欄にウクライナと書けば，手数料はかかりません。払込の口座番号は，　00190-5-31000　です。

このページのトップに戻る

　６．わが家の愛犬 チコ ちゃん
　　(11月9日 '21　記）
　　　　我家の愛犬チコちゃんは，2020年2月7日に家族の一員になりました。すごいワイルドな女の子でっす。野生児と呼んでいます。
　　　NHKのチコちゃんと同じ名前になって，すみません。5歳のチコちゃん許してね。

　　　　　生年月日：　2019年9月11日，　　マルチーズ（母）とプードル（父）の混血です。
　　　　　2021年11月7日現在（2歳と2か月）：　体高（4つ足で立っているときの地面から背までの長さ）24cm，
　　　　　　　　　 　　　　　　　　　　　 　　　体長（胸からお尻までの長さ）27cm,　　　体重：2.5kg　

　　　　　好きな遊び：鬼ごっこ（絶対つかまりません），シャドウボクシング（我々の服も破れるくらい）
　　　　　好きな食べ物：　リンゴとかき（柿）
　　　　　おしっことウンチは，ほとんど家の中でする。外では，我慢できなくなったときだけしますね。
　　　　　大人にはなつかないが，小さな子供（5,6才までの）は好きですね。
　　　これから時々，写真のっけます。

　
　　（1月12日　'22　記）
　　　　去年の12月頃から（2歳3か月時点）マーキングのオシッコをするようになりました。自分の縄張りを主張しているんですかね？
　　　しかし，ウンチはほとんど外ではしませんね。我々が食事をしているとき，よくウンチをしますね，なぜですかね？　なんか意味があるよね。
　　　　近所には，チコちゃんの友達は数匹います。好き嫌いがはっきりしているので，友達は少ない方だと思います。大好きなボーイフレンドが
　　　います。散歩中に見つけると，急突進してボディコンタクトします。敵は恐れをなして，若干身をよけますね（しかし，すごく楽しそうです）。
　　　とは言うものの，ボーイフレンドの飼い主さんのおやつが目的かもしれませんがね‥‥？？

　 　
　７．さいごに。　おとといのジョーは，77歳のじいさまです。団塊の世代（昭和21年〜昭和26年生まれ ？）の一人で，日本の高度成長期の真っ
　　ただ中，競争社会の中を落ちこぼれもせずに大学院まで進み，29歳のとき教育・研究の世界にもぐりこみ，もがきながらそして楽しみながら
　　36年間の教員生活を全うしました（数学者としては三流ですね）。社会や政治のことをゆっくり考えることはできなかった（もちろん，真剣に
　　考えていた真面目な or 過激な仲間も沢山いた）ので，皆にえばれるような人間ではないね。今の日本のよくない側面を作ってきた輩（やから）
　　と言われてもしょうがないね。このような反省をこめて，この独り言を書いています。

　　　このホームページのアップデイトは，年に数回はあると思います。数学勉強部屋のテキストの公開，入試問題の略解と解説などは，私に残された
　　大切な仕事だと思っています。おとといのジョーの独り言も追加するかもしれません。　　ではまた．．．Take care ... !

　　　　　　　　　New
　　（令和6年3月16日記）今年の2月19日，3月4日，5日に目の手術をしました（白内障は両眼，黄斑上膜は左眼）。名医の誉れ高い深作秀春先生
　　（深作眼科院長）に執刀してもらいました。手術後11日しか経っていませんが，今パソコンでホームページをアップデートしています。手術後の
　　経過は大変順調です。裸眼で近くも遠くもよく見えるようになってきました。ガチャ目でど近眼・老眼だった私が，メガネの必要がなくなったのは
　　驚きです。深作先生に感謝！！
　
　　ご意見，質問などは掲示板でどうぞ。
このページのトップに戻る 　第1ルームの目次に戻る
♠øøøøøøøøøøøø♣ℵℵℵ ℵℵℵℵℵℵℵ♥ββββββββββ ♦ξξξξξξξξξξ♠∇∇∇∇∇∇∇∇∇∇ ♣ℜℜℜℜℜℜℜℜℜℜ♥ΘΘΘΘΘΘΘ ΘΘΘΘΘΘ♦

inserted by FC2 system